Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T07:37:29.441Z Has data issue: false hasContentIssue false
  • English
  • Français

ALTERNATING COLOURINGS OF THE VERTICES OF A REGULAR POLYGON

Part of: Elementary number theory Graph theory Algebraic combinatorics Combinatorics

Published online by Cambridge University Press:  13 February 2019

SHIVANI SINGH  and
YULIYA ZELENYUK
SHIVANI SINGH
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag 3, Wits, 2050, Johannesburg, South Africa email [email protected]
YULIYA ZELENYUK*
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag 3, Wits, 2050, Johannesburg, South Africa email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

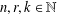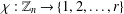Let $n,r,k\in \mathbb{N}$. An $r$-colouring of the vertices of a regular $n$-gon is any mapping $\unicode[STIX]{x1D712}:\mathbb{Z}_{n}\rightarrow \{1,2,\ldots ,r\}$. Two colourings are equivalent if one of them can be obtained from another by a rotation of the polygon. An $r$-ary necklace of length $n$ is an equivalence class of $r$-colourings of 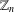$\mathbb{Z}_{n}$. We say that a colouring is 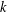$k$-alternating if all 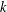$k$ consecutive vertices have pairwise distinct colours. We compute the smallest number $r$ for which there exists a 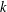$k$-alternating $r$-colouring of 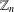$\mathbb{Z}_{n}$ and we count, for any $r$, 2-alternating $r$-colourings of 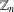$\mathbb{Z}_{n}$ and 2-alternating $r$-ary necklaces of length $n$.

Keywords

regular polygoncolouringnecklacealternatingBurnside’s lemma

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05A15: Exact enumeration problems, generating functions 05E18: Group actions on combinatorial structures 11A25: Arithmetic functions; related numbers; inversion formulas
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 177 - 181
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by NRF grant 107867 and the second author was supported by NRF grant IFR1202220164.

References

Aigner, M., Combinatorial Theory (Springer, Berlin–Heidelberg–New York, 1979).10.1007/978-1-4615-6666-3Google Scholar
Bender, E. and Goldman, J., ‘On the applications of Möbius inversion in combinatorial analysis’, Amer. Math. Monthly 82 (1975), 789–803.Google Scholar
Reed, R., ‘An introduction to chromatic polynomials’, J. Combin. Theory 4 (1968), 52–71.Google Scholar
Zelenyuk, Y. and Zelenyuk, Yu., ‘Counting symmetric bracelets’, Bull. Aust. Math. Soc. 89 (2014), 431–436.10.1017/S0004972713000701Google Scholar
Zelenyuk, Y. and Zelenyuk, Y., ‘Counting symmetric colourings of the vertices of a regular polygon’, Bull. Aust. Math. 90 (2014), 1–8.10.1017/S0004972713001147Google Scholar