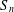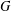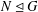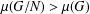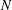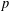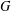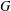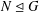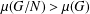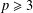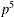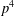5 results
16 - A Family of 4-Polytopes
- from IV - Miscellaneous Polytopes
-
- Book:
- Geometric Regular Polytopes
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 530-545
-
- Chapter
- Export citation
SUBGROUPS WITH NO ABELIAN COMPOSITION FACTORS ARE NOT DISTINGUISHED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 446-452
- Print publication:
- June 2020
-
- Article
- Export citation
MINIMAL EXCEPTIONAL
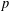 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 434-438
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
ON MINIMAL DEGREES OF PERMUTATION REPRESENTATIONS OF ABELIAN QUOTIENTS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 408-413
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
The Transfer in the Invariant Theory of Modular Permutation Representations II
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 2 / 01 June 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 272-282
- Print publication:
- 01 June 2002
-
- Article
-
- You have access
- Export citation