Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T11:39:46.614Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBGROUPS WITH NO ABELIAN COMPOSITION FACTORS ARE NOT DISTINGUISHED

Part of: Permutation groups

Published online by Cambridge University Press:  13 September 2019

ROBERT CHAMBERLAIN Open the ORCID record for ROBERT CHAMBERLAIN [Opens in a new window]
ROBERT CHAMBERLAIN*
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a finite group 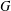$G$, define the minimal degree 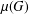$\unicode[STIX]{x1D707}(G)$ of 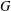$G$ to be the least $n$ such that 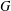$G$ embeds into 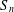$S_{n}$. We call 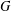$G$ exceptional if there is some 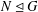$N\unlhd G$ with 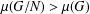$\unicode[STIX]{x1D707}(G/N)>\unicode[STIX]{x1D707}(G)$, in which case we call 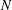$N$ distinguished. We prove here that a subgroup with no abelian composition factors is not distinguished.

Keywords

permutation representationfinite group

MSC classification

Primary: 20B05: General theory for finite groups
Secondary: 20B35: Subgroups of symmetric groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 3 , June 2020 , pp. 446 - 452
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the Engineering and Physical Sciences Research Council.

References

Becker, O., ‘The minimal degree of permutation representations of finite groups’, Preprint, 2012, arXiv:1204.1668.Google Scholar
Britnell, J. R., Saunders, N. and Skyner, T., ‘On exceptional groups of order p 5’, J. Pure Appl. Algebra 221(11) (2017), 2647–2665.10.1016/j.jpaa.2016.12.009Google Scholar
Cannon, J. J., Holt, D. F. and Unger, W. R., ‘The use of permutation representations in structural computations in large finite matrix groups’, J. Symbolic Comput. 95 (2019), 26–38.Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups (Oxford University Press, Eynsham, 1985), with computational assistance from J. G. Thackray.Google Scholar
Easdown, D. and Praeger, C. E., ‘On minimal faithful permutation representations of finite groups’, Bull. Aust. Math. Soc. 38(2) (1988), 207–220.10.1017/S0004972700027489Google Scholar
Guest, S., Morris, J., Praeger, C. E. and Spiga, P., ‘On the maximum orders of elements of finite almost simple groups and primitive permutation groups’, Trans. Amer. Math. Soc. 367(11) (2015), 7665–7694.10.1090/S0002-9947-2015-06293-XGoogle Scholar
Holt, D. F. and Walton, J., ‘Representing the quotient groups of a finite permutation group’, J. Algebra 248(1) (2002), 307–333.10.1006/jabr.2001.8961Google Scholar
Johnson, D. L., ‘Minimal permutation representations of finite groups’, Amer. J. Math. 93 (1971), 857–866.Google Scholar
Kovács, L. G. and Praeger, C. E., ‘On minimal faithful permutation representations of finite groups’, Bull. Aust. Math. Soc. 62(2) (2000), 311–317.Google Scholar
Lemieux, S., ‘Finite exceptional p-groups of small order’, Comm. Algebra 35(6) (2007), 1890–1894.Google Scholar
Neumann, P. M., ‘Some algorithms for computing with finite permutation groups’, in: Proc. Groups, St. Andrews, 1985, London Mathematical Society Lecture Note Series, 121 (Cambridge University Press, Cambridge, 1986), 59–92.Google Scholar
Wells, C., ‘Some applications of the wreath product construction’, Amer. Math. Monthly 83(5) (1975), 317–338.10.1080/00029890.1976.11994114Google Scholar
Wielandt, H., Finite Permutation Groups (Academic Press, New York–London, 1964), translated from the German by R. Bercov.Google Scholar