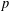Hostname: page-component-6bf8c574d5-nvqbz Total loading time: 0 Render date: 2025-03-07T18:03:58.444Z Has data issue: false hasContentIssue false
  • English
  • Français

MINIMAL EXCEPTIONAL $p$-GROUPS

Part of: Permutation groups

Published online by Cambridge University Press:  01 August 2018

ROBERT CHAMBERLAIN Open the ORCID record for ROBERT CHAMBERLAIN [Opens in a new window]
ROBERT CHAMBERLAIN*
Affiliation:
Mathematics Institute, University of Warwick, Coventry, CV4 7AL, UK email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a finite group 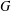$G$, denote by 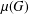$\unicode[STIX]{x1D707}(G)$ the degree of a minimal permutation representation of 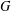$G$. We call 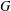$G$ exceptional if there is a normal subgroup 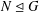$N\unlhd G$ with 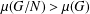$\unicode[STIX]{x1D707}(G/N)>\unicode[STIX]{x1D707}(G)$. To complete the work of Easdown and Praeger [‘On minimal faithful permutation representations of finite groups’, Bull. Aust. Math. Soc.38(2) (1988), 207–220], for all primes 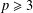$p\geq 3$, we describe an exceptional group of order 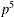$p^{5}$ and prove that no exceptional group of order 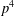$p^{4}$ exists.

Keywords

permutation representationfinite p-group

MSC classification

Primary: 20B05: General theory for finite groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 3 , December 2018 , pp. 434 - 438
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Easdown, D. and Praeger, C. E., ‘On minimal faithful permutation representations of finite groups’, Bull. Aust. Math. Soc. 38(2) (1988), 207–220.Google Scholar
Hall, M. Jr., The Theory of Groups (Chelsea Publishing Co., New York, 1976), reprint of the 1968 edition.Google Scholar