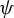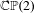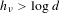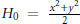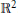12 results
MULTIPLE LOCAL AND GLOBAL BIFURCATIONS AND THEIR ROLE IN QUORUM SENSING DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 09 April 2025, e17
-
- Article
- Export citation
Spherical normal forms for germs of parabolic line biholomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-50
-
- Article
- Export citation
Satellites’ orbital stability through normal forms
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 15 / Issue S364 / October 2019
- Published online by Cambridge University Press:
- 30 May 2022, pp. 146-151
- Print publication:
- October 2019
-
- Article
-
- You have access
- Open access
- Export citation
Dimension of ergodic measures and currents on
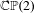 $\mathbb{C}\mathbb{P}(2)$
$\mathbb{C}\mathbb{P}(2)$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 04 January 2019, pp. 2131-2155
- Print publication:
- August 2020
-
- Article
- Export citation
ANALYTIC REDUCIBILITY OF RESONANT COCYCLES TO A NORMAL FORM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 27 November 2014, pp. 203-223
- Print publication:
- January 2016
-
- Article
- Export citation
On the relativistic Lagrange-Laplace secular dynamics for extrasolar systems
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 9 / Issue S310 / July 2014
- Published online by Cambridge University Press:
- 05 January 2015, pp. 74-77
- Print publication:
- July 2014
-
- Article
-
- You have access
- Export citation
The initial meadows
-
- Journal:
- The Journal of Symbolic Logic / Volume 75 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 12 March 2014, pp. 888-895
- Print publication:
- September 2010
-
- Article
- Export citation
Propagation of Gevrey regularity over long times for the fully discrete Lie Trotter splitting schemeapplied to the linear Schrödinger equation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 43 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 08 July 2009, pp. 651-676
- Print publication:
- July 2009
-
- Article
- Export citation
On the local structure of Dirac manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 774-786
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Normal forms for answer sets programming
-
- Journal:
- Theory and Practice of Logic Programming / Volume 5 / Issue 6 / November 2005
- Published online by Cambridge University Press:
- 31 October 2005, pp. 747-760
-
- Article
- Export citation
On complexity and motion planning for co-rank one sub-Riemannian metrics
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 10 / Issue 4 / October 2004
- Published online by Cambridge University Press:
- 15 October 2004, pp. 634-655
- Print publication:
- October 2004
-
- Article
- Export citation
Une classe d’hamiltoniens polynomiaux isochrones
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 3 / 01 September 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 323-334
- Print publication:
- 01 September 2001
-
- Article
-
- You have access
- Export citation