In his last paper, William Thurston defined the Master Teapot as the closure of the set of pairs  $(z,s)$, where s is the slope of a tent map
$(z,s)$, where s is the slope of a tent map  $T_s$ with the turning point periodic, and the complex number z is a Galois conjugate of s. In this case
$T_s$ with the turning point periodic, and the complex number z is a Galois conjugate of s. In this case  $1/z$ is a zero of the kneading determinant of
$1/z$ is a zero of the kneading determinant of  $T_s$. We remove the restriction that the turning point is periodic, and sometimes look beyond tent maps. However, we restrict our attention to zeros
$T_s$. We remove the restriction that the turning point is periodic, and sometimes look beyond tent maps. However, we restrict our attention to zeros  $x=1/z$ in the real interval
$x=1/z$ in the real interval  $(0,1)$. By the results of Milnor and Thurston, the kneading determinant has such a zero if and only if the map has positive topological entropy. We show that the first (smallest) zero is simple, but among other zeros there may be multiple ones. We describe a class of unimodal maps, so-called R-even ones, whose kneading determinant has only one zero in
$(0,1)$. By the results of Milnor and Thurston, the kneading determinant has such a zero if and only if the map has positive topological entropy. We show that the first (smallest) zero is simple, but among other zeros there may be multiple ones. We describe a class of unimodal maps, so-called R-even ones, whose kneading determinant has only one zero in  $(0,1)$. In contrast, we show that generic mixing tent maps have kneading determinants with infinitely many zeros in
$(0,1)$. In contrast, we show that generic mixing tent maps have kneading determinants with infinitely many zeros in  $(0,1)$. We prove that the second zero in
$(0,1)$. We prove that the second zero in  $(0,1)$ of the kneading determinant of a unimodal map, provided it exists, is always greater than or equal to
$(0,1)$ of the kneading determinant of a unimodal map, provided it exists, is always greater than or equal to  $\sqrt [3]{1/2}$, and if the kneading sequence begins with
$\sqrt [3]{1/2}$, and if the kneading sequence begins with  $RL^NR$,
$RL^NR$,  $N\geq 2$, then the best lower bound for the second zero is in fact
$N\geq 2$, then the best lower bound for the second zero is in fact  $\sqrt [N+1]{1/2}$. We also investigate (partially numerically) the shape of the Real Teapot, consisting of the pairs
$\sqrt [N+1]{1/2}$. We also investigate (partially numerically) the shape of the Real Teapot, consisting of the pairs  $(s,x)$, where x in
$(s,x)$, where x in  $(0,1)$ is a zero of the kneading determinant of
$(0,1)$ is a zero of the kneading determinant of  $T_s$, and
$T_s$, and  $s\in (1,2]$.
$s\in (1,2]$.
 $\mathcal {S}$-adic subshifts
$\mathcal {S}$-adic subshifts
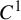 $C^{1}$ weakly conformal IFSs with overlaps
$C^{1}$ weakly conformal IFSs with overlaps