Hostname: page-component-5cf477f64f-pw477 Total loading time: 0 Render date: 2025-04-07T06:51:17.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Borel complexity of sets of points with prescribed Birkhoff averages in Polish dynamical systems with a specification property

Part of: Set theory Connections with other structures, applications Topological dynamics

Published online by Cambridge University Press:  02 April 2025

KONRAD DEKA Open the ORCID record for KONRAD DEKA [Opens in a new window] ,
STEVE JACKSON Open the ORCID record for STEVE JACKSON [Opens in a new window] ,
DOMINIK KWIETNIAK Open the ORCID record for DOMINIK KWIETNIAK [Opens in a new window]  and
BILL MANCE Open the ORCID record for BILL MANCE [Opens in a new window]
KONRAD DEKA*
Affiliation:
Faculty of Mathematics and Computer Science, Jagiellonian University in Krakow, ul. Łojasiewicza 6, 30-348 Kraków, Poland (e-mail: [email protected])
STEVE JACKSON
Affiliation:
Department of Mathematics, University of North Texas, General Academics Building 435, 1155 Union Circle, #311430, Denton, TX 76203-5017, USA (e-mail: [email protected])
DOMINIK KWIETNIAK
Affiliation:
Faculty of Mathematics and Computer Science, Jagiellonian University in Krakow, ul. Łojasiewicza 6, 30-348 Kraków, Poland (e-mail: [email protected])
BILL MANCE
Affiliation:
Faculty of Mathematics and Computer Science, Adam Mickiewicz University, ul. Umultowska 87, 61-614 Poznań, Poland (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the descriptive complexity of sets of points defined by restricting the statistical behaviour of their orbits in dynamical systems on Polish spaces. Particular examples of such sets are the sets of generic points of invariant Borel probability measures, but we also consider much more general sets (for example, 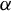$\alpha $-Birkhoff regular sets and the irregular set appearing in the multifractal analysis of ergodic averages of a continuous real-valued function). We show that many of these sets are Borel in general, and all these are Borel when we assume that our space is compact. We provide examples of these sets being non-Borel, properly placed at the first level of the projective hierarchy (they are complete analytic or co-analytic). This proves that the compactness assumption is, in some cases, necessary to obtain Borelness. When these sets are Borel, we measure their descriptive complexity using the Borel hierarchy. We show that the sets of interest are located at most at the third level of the hierarchy. We also use a modified version of the specification property to show that these sets are properly located at the third level of the hierarchy for many dynamical systems. To demonstrate that the specification property is a sufficient, but not necessary, condition for maximal descriptive complexity of a set of generic points, we provide an example of a compact minimal system with an invariant measure whose set of generic points is 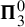$\boldsymbol {\Pi }^0_3$-complete.

Keywords

generic pointsspecification propertyBorel hierarchy

MSC classification

Primary: 54H05: Descriptive set theory (topological aspects of Borel, analytic, projective, etc. sets)
Secondary: 03E15: Descriptive set theory 37B10: Symbolic dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 29
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Airey, D., Jackson, S., Kwietniak, D. and Mance, B.. Borel complexity of sets of normal numbers via generic points in subshifts with specification. Trans. Amer. Math. Soc. 373(7) (2020), 4561–4584.CrossRefGoogle Scholar
Airey, D., Jackson, S. and Mance, B.. Some complexity results in the theory of normal numbers. Canad. J. Math. 74(1) (2022), 170–198.Google Scholar
Barreira, L., Saussol, B. and Schmeling, J.. Distribution of frequencies of digits via multifractal analysis. J. Number Theory 97(2) (2002), 410–438.CrossRefGoogle Scholar
Becher, V., Heiber, P. A. and Slaman, T. A.. Normal numbers and the Borel hierarchy. Fund. Math. 226(1) (2014), 63–78.CrossRefGoogle Scholar
Becher, V. and Slaman, T. A.. On the normality of numbers to different bases. J. Lond. Math. Soc. (2) 90(2) (2014), 472–494.Google Scholar
Beros, K. A.. Normal numbers and completeness results for difference sets. J. Symb. Log. 82(1) (2017), 247–257.CrossRefGoogle Scholar
Bogachev, V. I.. Measure Theory. Vols. I, II. Springer-Verlag, Berlin, 2007.CrossRefGoogle Scholar
Bowen, R.. Periodic points and measures for Axiom $\mathrm{A}$ diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Cyr, V. and Kra, B.. Counting generic measures for a subshift of linear growth. J. Eur. Math. Soc. (JEMS) 21(2) (2019), 355–380.CrossRefGoogle Scholar
Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527). Springer-Verlag, Berlin, 1976.CrossRefGoogle Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Algebraic and Topological Dynamics. Ed. Kolyada, S., Manin, Y. and Ward, T.. American Mathematical Society, Providence, RI, 2005, pp. 7–37.Google Scholar
Eggleston, H. G.. The fractional dimension of a set defined by decimal properties. Quart. J. Math. Oxford Ser. 20 (1949), 31–36.Google Scholar
Fan, A.-H., Feng, D.-J. and Wu, J.. Recurrence, dimension and entropy. J. Lond. Math. Soc. (2) 64(1) (2001), 229–244.CrossRefGoogle Scholar
Garling, D. J. H.. Analysis on Polish Spaces and an Introduction to Optimal Transportation (London Mathematical Society Student Texts, 89). Cambridge University Press, Cambridge, 2018.Google Scholar
Grivaux, S. and Matheron, É.. Invariant measures for frequently hypercyclic operators. Adv. Math. 265 (2014), 371–427.CrossRefGoogle Scholar
Iommi, G., Todd, M. and Velozo, A.. Escape of entropy for countable Markov shifts. Adv. Math. 405 (2022), Paper No. 108507.Google Scholar
Iommi, G. and Velozo, A.. The space of invariant measures for countable Markov shifts. J. Anal. Math. 143(2) (2021), 461–501.CrossRefGoogle Scholar
Jackson, S., Mance, B. and Roth, S.. A non-Borel special alpha-limit set in the square. Ergod. Th. & Dynam. Sys. 42(8) (2022), 2550–2560.Google Scholar
Kechris, A. S.. Classical Descriptive Set Theory (Graduate Texts in Mathematics, 156). Springer-Verlag, New York, 1995.Google Scholar
Ki, H. and Linton, T.. Normal numbers and subsets of $\mathbf{N}$ with given densities. Fund. Math. 144(2) (1994), 163–179.Google Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences. Dover, Mineola, NY, 2006.Google Scholar
Kwietniak, D., Ła̧cka, M. and Oprocha, P.. A panorama of specification-like properties and their consequences. Dynamics and Numbers (Contemporary Mathematics, 669). Ed. S. Kolyada, M. Möller, P. Moree and T. Ward. American Mathematical Society, Providence, RI, 2016, pp. 155–186.CrossRefGoogle Scholar
Kwietniak, D. and Ubik, M.. Topological entropy of compact subsystems of transitive real line maps. Dyn. Syst. 28(1) (2013), 62–75.CrossRefGoogle Scholar
Lind, D. A.. Dynamical properties of quasihyperbolic toral automorphisms. Ergod. Th. & Dynam. Sys. 2(1) (1982), 49–68.CrossRefGoogle Scholar
Łuczak, T.. On the fractional dimension of sets of continued fractions. Mathematika 44(1) (1997), 50–53.CrossRefGoogle Scholar
Marcus, B.. A note on periodic points for ergodic Toral automorphisms. Monatsh. Math. 89(2) (1980), 121–129.Google Scholar
Olsen, L.. Applications of multifractal divergence points to sets of numbers defined by their $N$ -adic expansion. Math. Proc. Cambridge Philos. Soc. 136(1) (2004), 139–165.CrossRefGoogle Scholar
Olsen, L.. On the ${\Pi}_{\unicode{x3b3}}^0$ -completeness and ${\Sigma}_{\unicode{x3b3}}^0$ -completeness of multifractal decomposition sets. Mathematika 64(1) (2018), 77–114.CrossRefGoogle Scholar
Oxtoby, J. C.. Ergodic sets. Bull. Amer. Math. Soc. 58 (1952), 116–136.Google Scholar
Pfister, C. E. and Sullivan, W. G.. Large deviations estimates for dynamical systems without the specification property. Applications to the $\beta$ -shifts. Nonlinearity 18(1) (2005), 237–261.Google Scholar
Sarig, O. M.. Phase transitions for countable Markov shifts. Comm. Math. Phys. 217(3) (2001), 555–577.Google Scholar
Tomaszewski, J.. Borel complexity of the set of typical numbers. Topology Appl. 345 (2024), Paper No. 108836, 12 pp.CrossRefGoogle Scholar
Usachev, A.. Hausdorff dimension of the set of almost convergent sequences. Glasg. Math. J. 64(3) (2022), 691–697.CrossRefGoogle Scholar
Wang, B.-W. and Wu, J.. Hausdorff dimension of certain sets arising in continued fraction expansions. Adv. Math. 218(5) (2008), 1319–1339.CrossRefGoogle Scholar