Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T19:06:54.767Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical Diophantine approximation and shrinking targets for 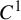$C^{1}$ weakly conformal IFSs with overlaps

Part of: Diophantine approximation, transcendental number theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  10 February 2025

EDOUARD DAVIAUD
EDOUARD DAVIAUD*
Affiliation:
Université Paris-Est, LAMA (UMR 8050) UPEMLV, UPEC, CNRS, F-94010 Créteil, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we extend, with a great deal of generality, many results regarding the Hausdorff dimension of certain dynamical Diophantine coverings and shrinking target sets associated with a conformal iterated function system (IFS) previously established under the so-called open set condition. The novelty of the result we present is that it holds regardless of any separation assumption on the underlying IFS and thus extends to a large class of IFSs the previous results obtained by Beresnevitch and Velani [A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2) 164(3) (2006), 971–992] and by Barral and Seuret [The multifractal nature of heterogeneous sums of Dirac masses. Math. Proc. Cambridge Philos. Soc. 144(3) (2008), 707–727]. Moreover, it will be established that if S is conformal and satisfies mild separation assumptions (which are, for instance, satisfied for any self-similar IFS on 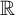$\mathbb {R}$ with algebraic parameters, no exact overlaps and similarity dimension smaller than 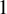$1$), then the classical result of Hill–Velani regarding the shrinking target problem associated with a conformal IFS satisfying the open set condition (and for which the Hausdorff measure was later computed by Allen and Barany [On the Hausdorff measure of shrinking target sets on self-conformal sets. Mathematika 67 (2021), 807–839]) can be extended.

Keywords

Diophantine approximation approximationsfractal geometrydynamical coverings

MSC classification

Primary: 11J83: Metric theory 37D35: Thermodynamic formalism, variational principles, equilibrium states
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 50
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, D. and Bárány, S.. On the Hausdorff measure of shrinking target sets on self-conformal sets. Mathematika 67 (2021), 807–839.CrossRefGoogle Scholar
Baker, S.. Intrinsic Diophantine approximation for overlapping iterated function systems. Math. Ann. 388 (2024), 3259–3297.CrossRefGoogle Scholar
Bandt, C., Viet Hung, N. and Rao, H.. On the open set condition for self-similar fractals. Proc. Amer. Math. Soc. 287 (2005), 1369–1374.CrossRefGoogle Scholar
Barral, J. and Feng, D.. On multifractal formalism for self-similar measures with overlaps. Math. Z. 298 (2021), 359–383.CrossRefGoogle Scholar
Barral, J. and Seuret, S.. Heterogeneous ubiquitous systems in ${\mathbb{R}}^d$ and Hausdorff dimensions. Bull. Braz. Math. Soc. (N.S.) 38(3) (2007), 467–515.CrossRefGoogle Scholar
Barral, J. and Seuret, S.. The multifractal nature of heterogeneous sums of Dirac masses. Math. Proc. Cambridge Philos. Soc. 144(3) (2008), 707–727.CrossRefGoogle Scholar
Beresnevitch, V. and Velani, S.. A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2) 164(3) (2006), 971–992.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer-Verlag, Berlin, 1975, no. 236, pp. 121–153.CrossRefGoogle Scholar
Brown, G., Michon, G. and Peyrière, J.. On the multifractal analysis of measures. J. Stat. Phys. 66 (1992), 775–790.CrossRefGoogle Scholar
Daviaud, E.. A dimensional mass transference principle for Borel probability measures and applications. Preprint, 2022, arXiv:2204.01302.Google Scholar
Daviaud, E.. A note about Diophantine approximation by rational polynomial in t. Available on ResearchGate, 2023, doi: 10.13140/RG.2.2.16861.18401.CrossRefGoogle Scholar
Daviaud, E.. An upper-bound for the Hausdorff dimension of limsup sets. Real Anal. Exchange 49 (2024), 259–292.CrossRefGoogle Scholar
Daviaud, E.. Limsup of balls of full finite measure and covering properties. Available on ResarchGate, 2024, doi: 10.13140/RG.2.2.34656.29443.CrossRefGoogle Scholar
Eriksson-Bique, S.. A new Hausdorff content bound for limsup sets. Adv. Math. 445 (2022), 109638.CrossRefGoogle Scholar
Falconer, K.. Fractal Geometry. John Wiley & Sons, Hoboken, NJ, 1990.Google Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications, 2nd edn. John Wiley & Sons, Inc., Hoboken, NJ, 2003.CrossRefGoogle Scholar
Fan, A.-H., Schmeling, J. and Troubetzkoy, S.. A multifractal mass transference principle for Gibbs measures with applications to dynamical diophantine approximation. Proc. Lond. Math. Soc. (3) 107(5) (2013), 1173–1219.CrossRefGoogle Scholar
Feng, D.. Gibbs properties of self-conformal measures and the multifractal formalism. Ergod. Th. & Dynam. Sys. 27(3) (2007), 787–812.CrossRefGoogle Scholar
Feng, D. and Hu, H.. Dimension theory of iterated function systems. Comm. Pure Appl. Math. 62 (2009), 1435–1500.CrossRefGoogle Scholar
Fraser, J. and Stuart, L.. A new perspective on the Sullivan dictionary via Assouad type dimensions and spectra. Bull. Amer. Math. Soc. 61 (2024), 103–118.Google Scholar
Frisch, U. and Parisi, D.. Fully developed turbulence and intermittency in turbulence, and predictability in geophysical fluid dynamics and climate dynamics. International School of Physics “Enrico Fermi” (Course, 88). Ed. Ghil, M.. North Holland, Amsterdam, 1985, pp. 84–88.Google Scholar
Ghosh, A. and Nandi, D.. Diophantine approximation, large intersections and geodesics in negative curvature. Proc. London Math. Soc. 128 (2024), e12581.CrossRefGoogle Scholar
Hill, R. and Velani, S.. The ergodic theory of shrinking targets. Invent. Math. 119 (1995), 175–198.CrossRefGoogle Scholar
Hochman, M.. On self-similar sets with overlaps and inverse theorems for entropy in ${\mathbb{R}}^d$ . Mem. Amer. Math. Soc. 265 (2022).Google Scholar
Hutchinson, J. E.. Fractals and self similarity. Indiana Univ. Math. J. 30 (1981), 713–747.CrossRefGoogle Scholar
Koivusalo, H. and Rams, M.. Mass transference principle: from balls to arbitrary shapes. Int. Math. Res. Not. IMRN 2021 (2021), 6315–6330.CrossRefGoogle Scholar
Liao, L. and Seuret, S.. Diophantine approximation by orbits of expanding Markov maps. Ergod. Th. & Dynam. Sys. 33 (2013), 585–608.CrossRefGoogle Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces: Fractals and Rectifiability (Cambridge Studies in Advanced Mathematics, 44). Cambridge University Press, Cambridge, 1999.Google Scholar
Olsen, L.. Self-affine multifractal Sierpinski sponges in ${\mathbb{R}}^d$ . Pacific J. Math. 183 (1998), 143–199.CrossRefGoogle Scholar
Persson, T. and Rams, M.. On shrinking targets for piecewise expanding interval maps. Ergod. Th. & Dynam. Sys. 37 (2017), 646–663.CrossRefGoogle Scholar
Rapaport, A.. Proof of the exact overlaps conjecture for systems with algebraic contractions. Ann. Sci. Éc. Norm. Supér. (4) 55 (2022), 1357–1377.CrossRefGoogle Scholar
Rapaport, A. and Varju, P.. Self-similar measures associated to a homogeneous system of three maps. Duke Math. J. 173(3) (2024), 513–602.CrossRefGoogle Scholar
Rapaport, A. and Jordan, T.. Dimension of ergodic measures projected onto self-similar sets with overlaps. Proc. Lond. Math. Soc. (3) 122(2) (2021), 191–206.Google Scholar
Ruelle, D.. Thermodynamic Formalism. The Mathematical Structures of Classical Equilibrium Statistical Mechanics (Encyclopedia of Mathematics and Its Applications, 5). Addison-Wesley Publishing Co., Reading, MA, 1978.Google Scholar
Schief, A.. Separation properties for self-similar sets. Proc. Amer. Math. Soc. 122 (1994), 1.CrossRefGoogle Scholar
Shmerkin, P.. On Furstenberg’s intersection conjecture, self-similar measures, and the ${L}^q$ norms of convolutions. Ann. of Math. (2) 189(2) (2019), 319–391.CrossRefGoogle Scholar