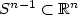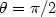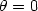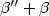Research Article
Is it wise to keep laminating?
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 452-477
-
- Article
- Export citation
The topological asymptotic expansion for the Quasi-Stokes problem
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 478-504
-
- Article
- Export citation
Slice convergence: stabilité et optimisation dans les espaces nonréflexifs
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 505-525
-
- Article
- Export citation
Reduction by group symmetry of second order variational problems on asemidirect product of Lie groups with positive definite Riemannian metric
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 526-548
-
- Article
- Export citation
Sharp summability for Monge Transport densityvia Interpolation
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 549-552
-
- Article
- Export citation
Control for the sine-gordon equation
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 553-573
-
- Article
- Export citation
Analysis and finite element error estimates for the velocitytracking problem for Stokes flows via a penalized formulation
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 574-592
-
- Article
- Export citation
Resonance of minimizers for n-level quantum systemswith an arbitrary cost
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 593-614
-
- Article
- Export citation
On harmonic disturbance rejection of an undamped Euler-Bernoulli beam with rigid tip body
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 615-623
-
- Article
- Export citation
Anisotropic functions: a genericity resultwith crystallographic implications
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 624-633
-
- Article
- Export citation
On complexity and motion planning for co-rank one sub-Riemannian metrics
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 634-655
-
- Article
- Export citation
A Γ-convergence result for variational integratorsof lagrangians with quadratic growth
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 656-665
-
- Article
- Export citation
Regularity along optimaltrajectories of the value function of a Mayer problem
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 666-676
-
- Article
- Export citation
Generic existence result for an eigenvalue problemwith rapidly growing principal operator
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 677-691
-
- Article
- Export citation