Here we provide a theoretical framework revealing that the radius 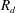 $R_{d}$ of the top droplet ejected from a bursting bubble of radius
$R_{d}$ of the top droplet ejected from a bursting bubble of radius  $R_{b}$ and
$R_{b}$ and 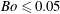 $Bo\leqslant 0.05$ can be expressed as
$Bo\leqslant 0.05$ can be expressed as 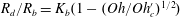 $R_{d}/R_{b}=K_{b}(1-(Oh/Oh_{c}^{\prime })^{1/2})$ for
$R_{d}/R_{b}=K_{b}(1-(Oh/Oh_{c}^{\prime })^{1/2})$ for 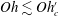 $Oh\lesssim Oh_{c}^{\prime }$ or as
$Oh\lesssim Oh_{c}^{\prime }$ or as 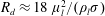 $R_{d}\approx 18\,\unicode[STIX]{x1D707}_{l}^{2}/(\unicode[STIX]{x1D70C}_{l}\unicode[STIX]{x1D70E})$ for
$R_{d}\approx 18\,\unicode[STIX]{x1D707}_{l}^{2}/(\unicode[STIX]{x1D70C}_{l}\unicode[STIX]{x1D70E})$ for 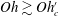 $Oh\gtrsim Oh_{c}^{\prime }$, with the numerically fitted constants
$Oh\gtrsim Oh_{c}^{\prime }$, with the numerically fitted constants  $K_{b}\approx 0.2$,
$K_{b}\approx 0.2$, 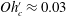 $Oh_{c}^{\prime }\approx 0.03$,
$Oh_{c}^{\prime }\approx 0.03$, 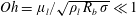 $Oh=\unicode[STIX]{x1D707}_{l}/\sqrt{\unicode[STIX]{x1D70C}_{l}\,R_{b}\,\unicode[STIX]{x1D70E}}\ll 1$ the Ohnesorge number,
$Oh=\unicode[STIX]{x1D707}_{l}/\sqrt{\unicode[STIX]{x1D70C}_{l}\,R_{b}\,\unicode[STIX]{x1D70E}}\ll 1$ the Ohnesorge number, 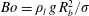 $Bo=\unicode[STIX]{x1D70C}_{l}\,g\,R_{b}^{2}/\unicode[STIX]{x1D70E}$ the Bond number, and
$Bo=\unicode[STIX]{x1D70C}_{l}\,g\,R_{b}^{2}/\unicode[STIX]{x1D70E}$ the Bond number, and 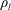 $\unicode[STIX]{x1D70C}_{l}$,
$\unicode[STIX]{x1D70C}_{l}$, 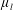 $\unicode[STIX]{x1D707}_{l}$ and
$\unicode[STIX]{x1D707}_{l}$ and  $\unicode[STIX]{x1D70E}$ indicating the liquid density, dynamic viscosity and interfacial tension coefficient, respectively. These predictions, which do not only have solid theoretical roots but are also much more accurate than the usual 10 % rule used in the context of marine spray generation via whitecaps for
$\unicode[STIX]{x1D70E}$ indicating the liquid density, dynamic viscosity and interfacial tension coefficient, respectively. These predictions, which do not only have solid theoretical roots but are also much more accurate than the usual 10 % rule used in the context of marine spray generation via whitecaps for 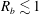 $R_{b}\lesssim 1$ mm, agree very well with both experimental data and numerical simulations for the values of
$R_{b}\lesssim 1$ mm, agree very well with both experimental data and numerical simulations for the values of 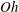 $Oh$ and
$Oh$ and 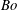 $Bo$ investigated. Moreover, making use of a criterion which reveals the mechanism that controls the growth rate of capillary instabilities, we also explain here why no droplets are ejected from the tip of the fast Worthington jet for
$Bo$ investigated. Moreover, making use of a criterion which reveals the mechanism that controls the growth rate of capillary instabilities, we also explain here why no droplets are ejected from the tip of the fast Worthington jet for 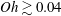 $Oh\gtrsim 0.04$. In addition, our results predict the generation of submicron-sized aerosol particles with diameters below 100 nm and velocities
$Oh\gtrsim 0.04$. In addition, our results predict the generation of submicron-sized aerosol particles with diameters below 100 nm and velocities 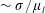 ${\sim}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}_{l}$ for bubble radii
${\sim}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}_{l}$ for bubble radii 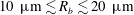 $10~\unicode[STIX]{x03BC}\text{m}\lesssim R_{b}\lesssim 20~\unicode[STIX]{x03BC}\text{m}$, within the range found in natural conditions and in good agreement with experiments – a fact suggesting that our study could be applied in the modelling of sea spray aerosol production.
$10~\unicode[STIX]{x03BC}\text{m}\lesssim R_{b}\lesssim 20~\unicode[STIX]{x03BC}\text{m}$, within the range found in natural conditions and in good agreement with experiments – a fact suggesting that our study could be applied in the modelling of sea spray aerosol production.