Article contents
Solitary waves in power-law deformable conduits with laminar or turbulent fluid flow
Published online by Cambridge University Press: 10 January 2020
Abstract
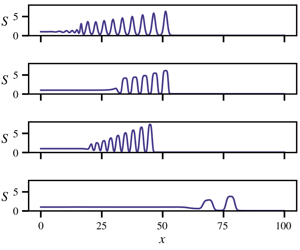
Fluid flow through pipe-like conduits embedded in viscously deformable material occurs in many natural systems, including magma transport in the Earth’s mantle and channelized water flow beneath glaciers. Here, we present and explore a model of fluid flow in viscously deformable conduits that unifies previously published models of magmatic and glacial systems. Previous results for magmatic systems have demonstrated the existence of solitary wave solutions for the case of laminar flow in Newtonian conduits. Here we extend these models to allow turbulent fluid flow in power-law materials consistent with models used in subglacial hydrology. The generalized model encompasses both laminar and turbulent fluid flow, and the solid matrix may deform according to any power-law rheology. A quasilinear approximation of the governing equations is introduced, along with an initial condition that develops into a perfect step shock. This initial condition is used in numerical solution of the full nonlinear system where a dispersive wave train forms at shock time. We show that solitary wave solutions exist for all parameters. Rheology-dependent flattening of the wave peaks is investigated. In the limit of a perfectly plastic matrix, the solitary waves approach square waves asymptotically. Motivated by subglacial hydrology models, we study the effect of discharge-dependent melting on evolution of the solitary waves. We find that melting focuses at the wave peaks, causing the waves to grow and accelerate over time.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 6
- Cited by


