Article contents
Linear stability of katabatic Prandtl slope flows with ambient wind forcing
Published online by Cambridge University Press: 08 January 2020
Abstract
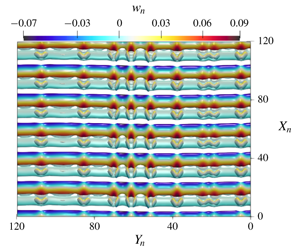
We investigate the stability of katabatic slope flows over an infinitely wide and uniformly cooled planar surface subject to a downslope uniform ambient wind aloft. We adopt an extension of Prandtl’s original model for slope flows (Lykosov & Gutman, Izv. Acad. Sci. USSR Atmos. Ocean. Phys., vol. 8 (8), 1972, pp. 799–809) to derive the base flow, which constitutes an interesting basic state in stability analysis because it cannot be reduced to a single universal form independent of external parameters. We apply a linear modal analysis to this basic state to demonstrate that for a fixed Prandtl number and slope angle, two independent dimensionless parameters are sufficient to describe the flow stability. One of these parameters is the stratification perturbation number that we have introduced in Xiao & Senocak (J. Fluid Mech., vol. 865, 2019, R2). The second parameter, which we will henceforth designate the wind forcing number, is hitherto uncharted and can be interpreted as the ratio of the kinetic energy of the ambient wind aloft to the damping due to viscosity and the stabilising effect of the background stratification. For a fixed Prandtl number, stationary transverse and travelling longitudinal modes of instabilities can emerge, depending on the value of the slope angle and the aforementioned dimensionless numbers. The influence of ambient wind forcing on the base flow’s stability is complicated, as the ambient wind can be both stabilising as well as destabilising for a certain range of the parameters. Our results constitute a strong counterevidence against the current practice of relying solely on the gradient Richardson number to describe the dynamic stability of stratified atmospheric slope flows.
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
Xiao and Senocak supplementary movie 1
Isocontour of Q-criterion when the longitudinal mode established at α=67⁰, Пs =13.8, √Пw ≈ 9 is subject to a sudden increase of √Пw ≈16. Flow becomes stabilized.
Xiao and Senocak supplementary movie 2
Isocontour of Q-criterion when the stable flow established at α=67⁰, Пs =13.8, √Пw ≈ 16 is subject to a sudden increase of √Пw ≈ 23. Transverse mode emerges.
Xiao and Senocak supplementary movie 3
Isocontour of Q-criterion when the longitudinal mode established at α=67⁰, Пs =16.5, √Пw ≈ 9 is subject to a sudden increase of √Пw ≈ 20. An additional transverse mode emerges.
Xiao and Senocak supplementary movie 4
Isocontour of Q-criterion when both longitudinal and transverse modes are established at α=67⁰, Пs =16.5, √Пw ≈ 20, then subject to a sudden increase of √Пw ≈ 30. Longitudinal mode gradually weakens so that only the transverse mode remains at the end.
- 4
- Cited by


