Article contents
Stability of ice lenses in saline soils
Published online by Cambridge University Press: 14 January 2020
Abstract
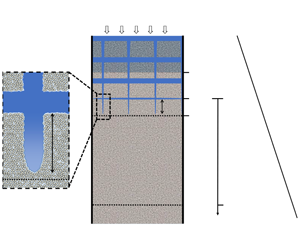
A model of the growth of an ice lens in a saline porous medium is developed. At high lens growth rates the pore fluid becomes supercooled relative to its equilibrium Clapeyron temperature. Instability occurs when the supercooling increases with distance away from the ice lens. Solute diffusion in the pore fluid significantly enhances the instability. An expression for the segregation potential of the soil is obtained from the condition for marginal stability of the ice lens. The model is applied to a clayey silt and a glass powder medium, indicating parameter regimes where the ice lens stability is controlled by viscous flow or by solute diffusion. A mushy layer, composed of vertical ice veins and horizontal ice lenses, forms in the soil in response to the instability. A marginal equilibrium condition is used to estimate the segregated ice fraction in the mushy layer as a function of the freezing rate and salinity.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 6
- Cited by


