We construct a type p with preweight ω with respect to itself in a theory with few types. A type with this property must be present in a stable theory with finitely many (but more than one) countable models. The construction is a modification of Hrushovski's important pseudoplane construction.

Since Georg Cantor discovered set theory the main problem in this area of mathematical research has been to discover what is the size of the continuum. The continuum hypothesis (CH) says that every infinite set of reals either has the same cardinality as the set of all reals or has the cardinality of the set of natural numbers, namely

In 1939 Kurt Gödel discovered the Constructible Universe and proved that CH holds in it. In the early sixties Paul Cohen proved that every universe of set theory can be extended to a bigger universe of set theory where CH fails. Moreover, given any reasonable cardinal κ, it is possible to build a model where the continuum size is κ. The new technique discovered by Cohen is called forcing and is being used successfully in other branches of mathematics (analysis, algebra, graph theory, etc.).

In the light of these two stupendous works the experts (especially the platonists) were forced to conclude that from the point of view of the classical axiomatization of set theory (called ZFC) it is impossible to give any answer to the continuum size problem: everything is possible!

In private communications Gödel suggested that the continuum size from a platonistic point of view should be ω2, the second uncountable cardinal. As this is not provable in ZFC, Gödel suggested that a new axiom should be added to ZFC to decide that the cardinality of the continuum is ω2.

We prove that any positive elementary (least fixed point) induction expressing the negation of transitive closure on finite nondirected graphs requires at least two recursion variables.

Let κ and λ be infinite cardinals, a filter on κ and a set of functions from κ to κ. The filter is generated by if consists of those subsets of κ which contain the range of some element of . The set is <λ-closed if it is closed in the <λ-topology on κκ. (In general, the <λ-topology on IA has basic open sets all such that, for all i ∈ I, Ui ⊆ A and ∣{i ∈ I: Ui ≠ A} ∣<λ.) The primary question considered in this paper asks “Is there a uniform ultrafilter on κ which is generated by a closed set of functions?” (Closed means <ω-closed.) We also establish the independence of two related questions. One is due to Carlson: “Does there exist a regular cardinal κ and a subtree T of <κκ such that the set of branches of T generates a uniform ultrafilter on κ?”; and the other is due to Pouzet: “For all regular cardinals κ, is it true that no uniform ultrafilter on κ is it true that no uniform ultrafilter on κ analytic?”

We show that if κ is a singular, strong limit cardinal, then there is a uniform ultrafilter on κ which is generated by a closed set of increasing functions. Also, from the consistency of an almost huge cardinal, we get the consistency of CH + “There is a uniform ultrafilter on ℵ1 which is generated by a closed set of increasing functions”. In contrast with the above results, we show that if Κ is any cardinal, λ is a regular cardinal less than or equal to κ and ℙ is the forcing notion for adding at least (κ<λ)+ generic subsets of λ, then in VP, no uniform ultrafilter on κ is generated by a closed set of functions.

We prove that a number of axioms, each a consequence of PFA (the Proper Forcing Axiom) are equivalent. In particular we show that TOP (the Thinning-out Principle as introduced by Baumgartner in the Handbook of set-theoretic topology), is equivalent to the following statement: If I is an ideal on ω1 with ω1 generators, then there exists an uncountable X ⊆ ω1, such that either [X]ω ∩ I = ∅ or [X]ω ⊆ I.

We define a σ-ideal on the set of functions ωω with the property that a real x ∈ ωω is a Hechler real over V if and only if x omits all Borel sets in . In fact we define a topology on ωω related to Hechler forcing such that is the family of first category sets in . We study cardinal invariants of the ideal .

We present in this paper an axiomatization of Belnap and Perloff's stit theory (a logic of “seeing to it that”) with a single agent. The idea of the proof is to apply the notion of companion sets—the same notion as used in another paper by the author that showed the decidability of stit theory with a single agent and Refref equivalence.

We study first-order properties of the quotient rings (V)/ by a prime ideal where (V) is the ring of p-adic valued continuous definable functions on some affine p-adic variety V. We show that they are integrally closed Henselian local rings, with a p-adically closed residue field and field of fractions, and they are not valuation rings in general but always satisfy ∀ x, y(x∣y2 ∨ y∣x2).

A definition is given for formulae A1, …, An in some theory T which is formalized in a propositional calculus S to be (in)dependent with respect to S. It is shown that, for intuitionistic propositional logic IPC, dependency (with respect to IPC itself) is decidable. This is an almost immediate consequence of Pitts’ uniform interpolation theorem for IPC. A reasonably simple infinite sequence of IPC-formulae Fn (p, q) is given such that IPC-formulae A and B are dependent if and only if at least on of the Fn (A, B) is provable.

Let P− denote the Peano axioms minus the induction scheme. Let IΣn, (I∏n), BΣn (B∏n), LΣn (L∏n denote the induction scheme, the collection scheme, and the least number principle for Σn-(∏n-) formulas respectively. Paris and Kirby [3] studied the relative proof-theoretic strengths of those schemes. The general theorem states that IΣn, I∏n, LΣn, and L∏n are equivalent; IΣn implies BΣn implies IΣn–1; but not conversely.

In recent years, people have been interested in doing recursion theory on fragments of arithmetic. One of the purposes of this study is to understand the priority methods. Much work has been done in this area. For example, M. Mytilinaios [5] showed that the Sacks splitting theorem can be proven in P− + IΣ1. Later, J. Mourad showed that the Sacks splitting theorem is indeed equivalent to IΣ1 [4]. M. Groszek and M. Mytilinaios [1] showed that P− + IΣ2 is sufficient to prove the existence of a high incomplete r.e. set. On the other hand, M. Mytilinaios and T. Slaman [6] showed that P− + IΣ1 is too weak to prove the existence of such a set. A natural question to ask is if the existence of such a set implies IΣ2. In this paper, we will show the answer is negative by constructing a model of P− + IΣ1 + ¬BΣ2 which has a high incomplete r.e. set. Notice that, as shown by M. Groszek and T. Slaman in [2], P− + IΣ1 is too weak to show the transitivity of weak Turing reducibility on Σ2-sets.

The κ-isomorphism property (IPκ) for nonstandard universes was introduced by Henson in [4]. There has been some recent effort aimed at more fully understanding this property. Jin and Shelah in [7] have shown that for κ < ⊐ω, IPκ is equivalent to what we will refer to as the κ-resplendence property. Earlier, in [6], Jin asked if IPκ is equivalent to IPℵ0 plus κ-saturation. He answered this question positively for κ = ℵ1. In this note we extend this answer to all κ. We also extend the result of Jin and Shelah to all κ. (Jin also observed this could be done.)

In order to strike a balance between the generalities of model theory and the specifics of nonstandard analysis, we will consider models of Zermelo set theory with the Axiom of Choice; we denote this theory by ZC. The axioms of ZC are just those of ZFC but without the replacement scheme. Thus, among the axioms of ZC are the power set axiom, the infinity axiom, the separation axioms and the axiom of choice.

Let(V, E) ⊨ ZC. If a ∈ V, we let *a = {x ∈ V: (V,E) ⊨ x ∈ a}. In particular, i ∈ *ω iff i ∈ V and (V,E) ⊨ (i is a natural number). A subset A ⊆ V is internal if A = *a for some a ∈ V.

The standard model of ZC consists of those sets of rank at most ω + ω. In other words, if we let V0 be the set of hereditarily finite sets and for n < ω, then (Vω, ∈) is the standard model of ZC, where Vω = ⋃n<ω. Vn.

The notion of logical reducibilities is derived from the idea of interpretations between theories. It was used by Lovász and Gács [LG77] and Immerman [Imm87] to give complete problems for certain complexity classes and hence establish new connections between logical definability and computational complexity.

However, the notion is also interesting in a purely logical context. For example, it is helpful to establish nonexpressibility results.

We say that a class 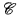of τ-structures is a >complete problem for a logic 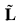under L-reductions if it is definable in 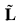[τ] and if every class definable in 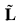can be ”translated” into 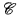by L-formulae (cf. §4).

We prove the following theorem:

1.1. Theorem. There are complete problems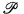for partial fixed-point logic and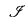for inductive fixed-point logic under quantifier-free reductions.

The main step of the proof is to establish a new normal form for fixed-point formulae (which might be of some interest itself). To obtain this normal form we use theorems of Abiteboul and Vianu [AV91a] that show the equivalence between the fixed-point logics we consider and certain extensions of the database query language Datalog.

In [Dah87] Dahlhaus gave a complete problem for least fixed-point logic. Since least fixed-point logic equals inductive fixed-point logic by a well-known result of Gurevich and Shelah [GS86], this already proves one part of our theorem.

However, our class 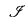gives a natural description of the fixed-point process of an inductive fixed-point formula and hence sheds some light on completely different aspects of the logic than Dahlhaus's construction, which is strongly based on the features of least fixed-point formulae.

If S, T are stationary subsets of a regular uncountable cardinal κ, we say that S reflects fully in T, S < T, if for almost all α ∈ T (except a nonstationary set) S ∩ α stationary in α. This relation is known to be a well-founded partial ordering. We say that a given poset P is realized by the reflection ordering if there is a maximal antichain 〈Xp: p ∈ P〉 of stationary subsets of Reg(κ) so that

We prove that if , and P is an arbitrary well-founded poset of cardinality ≤ κ+ then there is a generic extension where P is realized by the reflection ordering on κ.

On sait que par le choix d’ un langage suffisamment complexe, toute structure peut admettre une élimination des quantificateurs, malheureusement cette extension du langage peut nous éloigner des phénomènes algébriques. Nous allons nous intéresser à l’ élimination des quantificateurs pour des paires de corps. Dans le cas des paires de corps algébriquement clos et des paires denses de corps réel clos, on obtient une élimination en ajoutant au langage des prédicats ayant une signification algébrique: on peut les exprimer en disant que pour deux ensembles algébriques et donnés, il existe des points du sous-corps rationnels pour et pas pour , ou qu’ un ensemble semi-algébrique donné a des points rationnels sur le sous-corps. Robinson avait déjà abordé de façon informelle le cas des paires denses de corps réel-clos (cf. [Ro 2, p. 198]). Partant du langage des paires de corps ordonnés, enrichi de symboles de relations correspondant à l’ indépendance algébrique, il proposait d’ ajouter pas à pas des fonctions de Skolem Herbrand pour faire disparaitre les quantificateurs existentiels des formules, mais sans préciser le langage obtenu. Ici nous approchons le problème différemment en explicitant dès le départ le langage utilisé.

Grâce à ces résultats nous pourrons étudier le cas des paires séparées de corps réels clos ainsi que des paires de corps valués henseliens. En élargissant la définition d’ ensemble algébrique à tous les symboles du langage, les prédicats relationnels ajoutés ont la même signification que dans le cas des paires de corps algébriquement clos.

En comparant les techniques employées ici avec celles déjà utilisées dans [K], [B], [D 1] et [L], on remarque qu’il est possible de traîter une grande partie de l’ étude (complétude, modèle complétude, élimination des quantificateurs) des paires de corps algébriquement clos, réel-clos ou henseliens en se basant sur des prolongements d’ isomorphismes entre sous-structures dénombrables où l’ une des deux est contenue dans une structure ω1-saturée.

We give a self-contained geometric proof of the completeness theorem for the infinite-valued sentential calculus of Łukasiewicz.

The purpose of this paper is to show that semantics for relevance logic, based on the Routley-Meyer semantics, can be given without using the Routley star operator to treat negation. In the resulting semantics, negation is treated implicationally. It is shown that, by the use of restrictions on the ternary accessibility relation, simplified by the use of some definitions, a semantics can be stipulated over which R is complete.

Treating the existential quantification ∃νi as a diamond ♢i and the identity νi = νj as a constant δij, we study restricted versions of first order logic as if they were modal formalisms. This approach is closely related to algebraic logic, as the Kripke frames of our system have the type of the atom structures of cylindric algebras; the full cylindric set algebras are the complex algebras of the intended multidimensional frames called cubes.

The main contribution of the paper is a characterization of these cube frames for the finite-dimensional case and, as a consequence of the special form of this characterization, a completeness theorem for this class. These results lead to finite, though unorthodox, derivation systems for several related formalisms, e.g. for the valid n-variable first order formulas, for type-free valid formulas and for the equational theory of representable cylindric algebras. The result for type-free valid formulas indicates a positive solution to Problem 4.16 of Henkin, Monk and Tarski [16].

We study the I-ultrafilters on ω, where I is a a collection of subsets of a set X, usually ℝ or ω1. The I-ultrafilters usually contain the P-points, often as a small proper subset. We study relations between I-ultrafilters for various I, and closure of I-ultrafilters under ultrafilter sums. We consider, but do not settle, the question whether I-ultrafilters always exist.

Let us define the intuitionistic part of a classical theory T as the intuitionistic theory whose proper axioms are identical with the proper axioms of T. For example, Heyting arithmetic HA is the intuitionistic part of classical Peano arithmetic PA.

It's a well-known fact, proved by Heyting and Myhill, that ZF is identical with its intuitionistic part.

In this paper, we mainly prove that TT, Russell's Simple Theory of Types, and NF, Quine's “New Foundations,” are not equal to their intuitionistic part. So, an intuitionistic version of TT or NF seems more naturally definable than an intuitionistic version of ZF.

In the first section, we present a simple technique to build Kripke models of the intuitionistic part of TT (with short examples showing bad properties of finite sets if they are defined in the usual classical way).

In the remaining sections, we show how models of intuitionistic NF2 and NF can be obtained from well-chosen classical ones. In these models, the excluded middle will not be satisfied for some non-stratified sentences.