Symposium - International Astronomical Union, Dark Matter in the Universe
- This volume was published under a former title. See this journal's title history.
Research Article
Clustering Properties of Cold Dark Matter Universes and the CFA Redshift Survey: A Uniform Comparison
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 284
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Formation of Galactic Halos in the Cold Dark Matter Universe: Computer Simulations
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 285
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Formation of Large Scale Structure in the Explosion Scenario
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 286
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Profiles of Galaxy Clusters in Cosmological Scenarios
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 287
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Review Paper
Halos and Disk Stability
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 289-299
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Research Article
Massive Halos and the Stability of Hot Stellar Discs
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 300
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Global Stability of our Galaxy
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 301
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Review Paper
Observable Consequences of Triaxial Halos
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 303-313
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Research Article
Self-Gravitating Polar Ring Models
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 314
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Distribution of Dark Matter in Polar Ring Galaxies
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 315
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Halos around Ellipticals and the Environment Dependence of Hubble Type
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 316-317
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Review Paper
The Modified Newtonian Dynamics as an Alternative to Hidden Matter
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 319-333
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Research Article
Gravitational Channels and the Cosmological Constant A
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 334
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Review Paper
Galaxy Formation
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 335-359
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Research Article
Galaxy Formation in a Universe Dominated by Cold Dark Matter
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 360
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Embedding of Galactic Systems in Extended Neutrino Clouds
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 361
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Dwarf Galaxies, Cold Dark Matter, and Biased Galaxy Formation
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 362
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Hierarchical Clustering: Angular Momentum Density Anti-Correlation
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 363
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Formation of Galactic Halos in Universes Dominated by Cold Dark Matter
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 364
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Hydrogen Molecules and the Radiative Cooling of Pregalactic Shocks
-
- Published online by Cambridge University Press:
- 04 August 2017, p. 365
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service

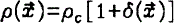 , where
, where 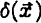 ) is a Gaussian process, then the mean run of density around a peak is proportional to the correlation function of
) is a Gaussian process, then the mean run of density around a peak is proportional to the correlation function of 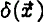 . If the mass about a peak comes to equilibrium in near-circular orbits, the exact equilibrium configuration can be calculated. The resulting rotation curve for a 1.5σ perturbation is shown as the curve HB in the figure below. As the baryon mass cools and condenses, it drags the CDM in with it, conserving the adiabatic invariants. Putting a 5×10
. If the mass about a peak comes to equilibrium in near-circular orbits, the exact equilibrium configuration can be calculated. The resulting rotation curve for a 1.5σ perturbation is shown as the curve HB in the figure below. As the baryon mass cools and condenses, it drags the CDM in with it, conserving the adiabatic invariants. Putting a 5×10