We consider the Yang–Mills functional denned on connections on a principal bundle over a compact Riemannian manifold of dimension 2 or 3. It is shown that if we consider the Yang–Mills functional as being defined on an appropriate Hilbert manifold of orbits of connections under the action of the group of principal bundle automorphisms, then the functional satisfies the Palais–Smale condition.

Let ℤ(G) be the integral group ring of the infinite dihedral group G; the aim is to calculate Autℤ(G), the group of Z-linear automorphisms of ℤ(G). It is shown that Aut ℤ(G), the subgroup of Aut *ℤ(G) consisting of those automorphisms that preserve elementwise the centre of ℤ(G), is a normal subgroup of Aut *ℤ(G) of index 2 and that Aut*ℤ(G) may be embedded monomorphically into M2(ℤ[t]), the ring of 2 × 2 matrices over a polynomial ring ℤ[t] From this embedding and by the Noether—Skolem Theorem it is shown that Inn (G), the group of inner automorphisms of ℤ(G) induced by the units of ℤ(G), is a normal subgroup of Aut*ℤ(G)/ such that Aut*ℤ(G)/Inn (G) is isomorphic to the Klein four-group.

In this paper we investigate integral transforms of type 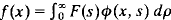, where φ(x, s) is the solution of the singular Sturm–Liouville problem: y″ + (s2 – q(x))y = 0, 0≦x <∞ with y(0) cos α + y′(0)sin α = 0, y(x) is bounded at ∞, and dp is the spectral measure. If F(s) = sk for some k = 0, 1, 2, …, then f(x) may not exist since, in general, φ(x, s) is not even in . One aim of this paper is to investigate the Abel summability of these integrals. In the special case where q(x) = 0 and α = π/2, then φ(x, s) = cos sx and dp = ds, while if α = 0, then φ(x, s) = −sin sx/s and dp = s2ds. It is known that

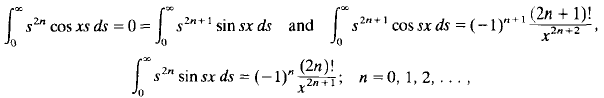
where the values of these integrals are interpreted as the Abel limits of these integrals or as the Fourier transform of some tempered distributions. Another aim of this paper is to derive the analogue of these results for the general kernel φ(x, s), and then apply that to the theory of asymptotic expansions.

This paper deals with two-point boundary-value problems for ordinary differential equations and the operators which they induce in the appropriate Hilbert space. The problems arenot required to be self-adjoint. No auxiliary condition such as Birkhoff-regularity is imposed. If T is such an operator, it may well have no meaningful spectral structure. It is shown, however, that when T is composed with its adjoint, the result is a non-negative self-adjoint differential operator. The eigenvalues and eigenfunctions of this composite operator are used to delineate the domain, action, range, and generalised inverse of T.

The equation studied here is Lny + p(x)y = 0, where Ln is a disconjugate differential operator and p(x) is of a fixed sign. We define a basis of the solution space and order its elements according to their relative magnitudes near infinity. Our method is independent of the possible oscillation or nonoscillation of the solutions and it is achieved by utilising the fact that some minors of the Wronskian never vanish.

The use of normal forms in the study of equilibria of vector fields and Hamiltonian systems is a well-established practice and is described in standard references (e.g. [1], [7] or [10]). Also well known is the fact that such normal forms are not unique, and the relationship between distinct normal forms of the same vector field has also been investigated, in particular by M. Kummer [8] and A. Brjuno [2,3] (also see [12]). In this paper we use this relationship to extract invariants of the vector field directly from an arbitrary normal form. The treatment is sufficiently general to handle the vector field and Hamiltonian cases simultaneously, and applications in these contexts are presented.

The formulation of our main result (Theorem 1.1) is reminiscent of, and was heavily influenced by, work of Shi Songling on planar vector fields [11]. Additional inspiration was provided by M. Kummer's contributions to the 1:1 resonance problem in [9]. The authors are grateful to Richard Cushman for comments on an earlier version of this paper.

This paper establishes the coexistence of small and large subharmonics in a special case of the ordinary non-linear differential equation

of order 2, where κ, ε are small parameters, λ>0 is a parameter independent of κ, ε, h(t) has the least period 2π and

It is divided into three sections. In Section 1 a general analysis of the periodic solutions of (.), classified into small, medium or large, is given. In Section 2 the general theory of Section 1 is applied to the special form of (.) where k = vε1+s, v>0, s>0 constants, to obtain results from which we extract in Section 2 a theorem (Section 3) on the coexistence of a small periodic solution of order 1, several small sub-harmonics and several large sub-harmonics of the special case

of (.), where Q≧1 is an integer.

We characterise all functions f meromorphic of finite order in the plane such that fF has only finitely many zeros, where F = f″ + αf for some constant α. The problem is related to results of N. Steinmetz and others.

We consider the effects of a small symmetry breaking perturbation on a system of differential equations near a Hopf bifurcation point, where the unperturbed system has O(2) symmetry. We show that there exist secondary bifurcations of invariant two-tori of solutions and that the flow on the tori can be quasiperiodic or weakly resonant (phase locked), depending on the size of the perturbation.

We consider a class of non-self adjoint multipoint eigenvalue problems. Using necessary conditions for the regularity of these problems, we obtain a theorem on the expansion of certain functions into a series of eigen- and associated functions.

In this paper we prove interior and global Hölder estimates for Lipschitz viscosity solutions of second order, nonlinear, uniformly elliptic equations. The smoothness hypotheses on the operators are more general than previously considered for classical solutions, so that our estimates are also new in this case and readily extend to embrace obstacle problems. In particular Isaac's equations of stochastic differential game theory constitute a special case of our results, and moreover our techniques, in combination with recent existence theorems of Ishii, lead to existence theorems for continuously differentiable viscosity solutions of the uniformly elliptic Isaac's equation.

We prove an existence theorem for a steady planar flow of an ideal fluid, containing a bounded symmetric pair of vortices, and approaching a uniform flow at infinity. The data prescribed are the rearrangement class of the vorticity field, and either the momentum impulse of the vortex pair, or the velocity of the vortex pair relative to the fluid at infinity. The stream function ψ for the flow satisfies the semilinear elliptic equation

in a half-plane bounded by the line of symmetry, where φ is an increasing function that is unknown a priori. The results are proved by maximising the kinetic energy over all flows whose vorticity fields are rearrangements of a specified function.

Conditions are obtained under which a graph G', obtained from a graph G by the attachment of a pendant edge, may be regarded as a perturbation of G. In this situation the index of G' is expressed as the sum of a convergent series whose terms are determined by the spectrum and certain angles of G.

In the recent past many results have been established on non-negative solutions to boundary value problems of the form

where λ>0, f(0)>0 (positone problems). In this paper we consider the impact on the non-negative solutions when f(0)<0. We find that we need f(u) to be convex to guarantee uniqueness of positive solutions, and f(u) to be appropriately concave for multiple positive solutions. This is in contrast to the case of positone problems, where the roles of convexity and concavity were interchanged to obtain similar results. We further establish the existence of non-negative solutions with interior zeros, which did not exist in positone problems.

In an earlier paper [8], I. J. Schoenberg discussed polynomial interpolation in one dimension at the points of a geometric progression, which was originally proposed by James Stirling. In the present paper, these ideas are generalised to two-dimensional polynomial interpolation at the points of a geometric mesh on a triangle. A Lagrange form is obtained for this interpolating polynomial and an algorithm is derived for evaluating it efficiently.

We consider the existence and smoothness of global centre unstable manifolds for finite and infinite dimensional flows or maps. We show that every global centre unstable manifold can be expressed as a graph of a Ck map, provided that the nonlinearities are Ck smooth. The proofs are based on a lemma by D. Henry on a necessary and sufficient condition for a Lipschitz map to be continuously differentiable.

Semilinear elliptic partial differential systems of second order with weak coupling are considered in exterior domains Ω ⊆ ℝN, N≧3. Conditions on the nonlinearities are given which guarantee the existence of solutions u with positive components in Ω such that u|∂Ω = 0 and u(x)→0 uniformly as |x|→∞. Asymptotic decay estimates for the solutions are established, including an exponential decay law under extra hypotheses.

In the paper referred to in the title [2] an open question was raised concerning the equality of the largest left hereditary radical and the largest right hereditary radical contained in each of certain radicals. In this addendum an affirmative answer is provided to this question.

Convergence criteria are derived for Aronszajn's method and for the Bazley-Fox C*C method applied to self-adjoint eigenvalue problems of the form Bx = λx. These criteria generalise previously used criteria and are seen to be, in a certain restricted sense, the best possible. The framework used is general enough to allow approximations where the intermediate problems are not finite dimensional perturbations of the base problem.

In this paper we give a characterisation of the multipliers of a space of almost convergent functions with respect to invariant means related to ergodic semigroups of operators. The characterisation extends several results of the literature.