Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T21:14:50.287Z Has data issue: false hasContentIssue false
  • English
  • Français

A system of order 2 in which small sub-harmonics and large sub-harmonics coexist

Published online by Cambridge University Press:  14 November 2011

Chike Obi
Chike Obi
Affiliation:
Mathematics Department, University of Lagos, Lagos, Nigeria
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper establishes the coexistence of small and large subharmonics in a special case of the ordinary non-linear differential equation

of order 2, where κ, ε are small parameters, λ>0 is a parameter independent of κ, ε, h(t) has the least period 2π and

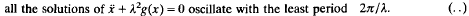
It is divided into three sections. In Section 1 a general analysis of the periodic solutions of (.), classified into small, medium or large, is given. In Section 2 the general theory of Section 1 is applied to the special form of (.) where k = vε1+s, v>0, s>0 constants, to obtain results from which we extract in Section 2 a theorem (Section 3) on the coexistence of a small periodic solution of order 1, several small sub-harmonics and several large sub-harmonics of the special case

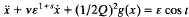
of (.), where Q≧1 is an integer.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 108 , Issue 1-2 , 1988 , pp. 35 - 44
Copyright
Copyright © Royal Society of Edinburgh 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Loud, W. S.. Periodic solutions of x” + cx' + g(x) = ef(t). Mem. Amer. Math. Soc. 31 (1959), 48–55.Google Scholar
2Obi, Chike. Analytical theory of non-linear oscillations I. Proc. Camb. Phil. Soc. 76 (1974), 285–296.CrossRefGoogle Scholar
3Obi, Chike. Analytical theory of non-linear oscillations II. SIAM J. Appl. Math. 31 (1976), 334–347.CrossRefGoogle Scholar
4Obi, Chike. Analytical theory of non-linear oscillations VIII. Ann. Mat. Pura Appl. 117 (1978), 339–347.CrossRefGoogle Scholar
5Obi, Chike. Analytical theory of non-linear oscillations IX. Ann. Mat. Pura Appl. 120 (1979), 139–157.CrossRefGoogle Scholar
6Obi, Chike. Analytical theory of non-linear oscillations X. Rend. Acad. Naz. XL Mem. Mat. Sci. Fis. Natur. 47 (1979), 53–56.Google Scholar