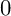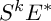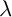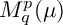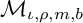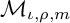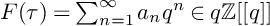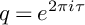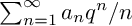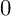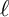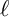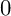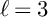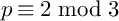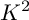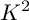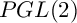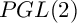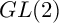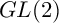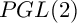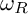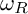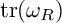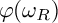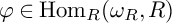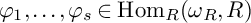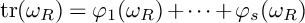Article
TAMARKIN–TSYGAN CALCULUS AND CHIRAL POISSON COHOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 751-765
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POSITIVELY CURVED FINSLER METRICS ON VECTOR BUNDLES
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2022, pp. 766-778
-
- Article
- Export citation
NORMAL HILBERT COEFFICIENTS AND ELLIPTIC IDEALS IN NORMAL TWO-DIMENSIONAL SINGULARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2022, pp. 779-800
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FRACTIONAL TYPE MARCINKIEWICZ INTEGRAL AND ITS COMMUTATOR ON NONHOMOGENEOUS SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2022, pp. 801-822
-
- Article
- Export citation
ON HIGHER TORSION CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2022, pp. 823-848
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAGNETIC (QUASI-)MODULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2022, pp. 849-864
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE BOUNDARY OF THE p-RANK
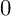 $0$
STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$
STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2022, pp. 865-887
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIRATIONAL RIGIDITY OF ORBIFOLD DEGREE 2 DEL PEZZO FIBRATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 02 June 2022, pp. 888-921
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SELMER GROUPS OF ELLIPTIC CURVES OVER THE
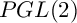 $PGL(2)$
EXTENSION
$PGL(2)$
EXTENSION
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2022, pp. 922-938
-
- Article
- Export citation
TRIPLE COVERS OF K3 SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2022, pp. 939-979
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SINGULAR HERMITIAN METRICS WITH ISOLATED SINGULARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2022, pp. 980-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLUTIONS OF THE tt*-TODA EQUATIONS AND QUANTUM COHOMOLOGY OF MINUSCULE FLAG MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2022, pp. 990-1004
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RINGS OF TETER TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2022, pp. 1005-1033
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
NMJ volume 248 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2022, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
NMJ volume 248 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation