Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T17:08:55.308Z Has data issue: false hasContentIssue false
  • English
  • Français

POSITIVELY CURVED FINSLER METRICS ON VECTOR BUNDLES

Part of: Geometric convexity Holomorphic fiber spaces Compact analytic spaces

Published online by Cambridge University Press:  08 March 2022

KUANG-RU WU Open the ORCID record for KUANG-RU WU [Opens in a new window]
KUANG-RU WU*
Affiliation:
Institute of Mathematics Academia Sinica Taipei Taiwan [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a convex and strongly pseudoconvex Kobayashi positive Finsler metric on a vector bundle E under the assumption that the symmetric power of the dual 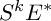$S^kE^*$ has a Griffiths negative 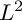$L^2$ -metric for some k. The proof relies on the negativity of direct image bundles and the Minkowski inequality for norms. As a corollary, we show that given a strongly pseudoconvex Kobayashi positive Finsler metric, one can upgrade to a convex Finsler metric with the same property. We also give an extremal characterization of Kobayashi curvature for Finsler metrics.

MSC classification

Primary: 32J25: Transcendental methods of algebraic geometry
Secondary: 32F17: Other notions of convexity 32L15: Bundle convexity
Type
Article
Information
Nagoya Mathematical Journal , Volume 248 , December 2022 , pp. 766 - 778
Check for updates
Copyright
© (2022) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aikou, T., A partial connection on complex Finsler bundles and its applications , Illinois J. Math. 42 (1998), 481–492.CrossRefGoogle Scholar
Aikou, Ta., Finsler Geometry on Complex Vector Bundles. A Sampler of Riemann–Finsler Geometry , Math. Sci. Res. Inst. Publ., 50, Cambridge University Press, Cambridge, 2004, 83–105.Google Scholar
Berndtsson, B., Curvature of vector bundles associated to holomorphic fibrations , Ann. of Math. (2) 169 (2009), 531–560.CrossRefGoogle Scholar
Berndtsson, B., Positivity of direct image bundles and convexity on the space of Kähler metrics , J. Differ. Geom. 81 (2009), 457–482.Google Scholar
Berndtsson, B. and Lempert, L., A proof of the Ohsawa-Takegoshi theorem with sharp estimates, J. Math. Soc. Japan 68 (2016), 1461–1472.CrossRefGoogle Scholar
Campana, F. and Flenner, H., A characterization of ample vector bundles on a curve , Math. Ann. 287 (1990), 571–575.CrossRefGoogle Scholar
Cao, J.-G. and Wong, P.-M., Finsler geometry of projectivized vector bundles , J. Math. Kyoto Univ. 43 (2003), 369–410.Google Scholar
Demailly, J.-P., “Pseudoconvex-concave duality and regularization of currents” in Several Complex Variables (Berkeley, CA, 1995–1996), Math. Sci. Res. Inst. Publ., 37, Cambridge University Press, Cambridge, 1999, 233–271.Google Scholar
Demailly, J.-P., Complex analytic and differential geometry, https://www-fourier.ujf-grenoble.fr/demailly/manuscripts/agbook.pdf, 2012.Google Scholar
Demailly, J.-P., Hermitian-Yang-Mills approach to the conjecture of Griffiths on the positivity of ample vector bundles, preprint, arXiv:2002.02677 Google Scholar
Deng, F., Wang, Z., Zhang, L., and Zhou, X., New characterizations of plurisubharmonic functions and positivity of direct image sheaves, preprint, arxiv:1809.10371 Google Scholar
Finski, S., On Monge–Ampère volumes of direct images , Int. Math. Res. Notices (2021), rnab058, 1–24.Google Scholar
Feng, H., Liu, K., and Wan, X., Chern forms of holomorphic Finsler vector bundles and some applications , Int. J. Math. 27 (2016), 1650030.CrossRefGoogle Scholar
Feng, H., Liu, K., and Wan, X., A Donaldson type functional on a holomorphic Finsler vector bundle , Math. Ann. 369 (2017), 997–1019.CrossRefGoogle Scholar
Feng, H., Liu, K., and Wan, X., Complex Finsler vector bundles with positive Kobayashi curvature, preprint, arXiv:1811.08617 Google Scholar
Griffiths, P. A., Hermitian Differential Geometry, Chern Classes, and Positive Vector Bundles, Global Analysis (Papers in Honor of K. Kodaira), University of Tokyo Press, Tokyo, 1969, 185–251.Google Scholar
Guan, Q. and Zhou, X., A solution of an $\ {L}^2\ {}$ extension problem with an optimal estimate and applications , Ann. of Math. (2) 181 (2015), 1139–1208.CrossRefGoogle Scholar
Hartshorne, R., Ample vector bundles , Inst. Hautes Études Sci. Publ. Math. (1966), no. 29, 63–94.Google Scholar
Hacon, C., Popa, M., and Schnell, C., Algebraic fiber spaces over abelian varieties: Around a recent theorem by Cao and P $\breve{\mathrm{a}}$ un, in Local and Global Methods in Algebraic Geometry, Contemp. Math., 712, American Mathematical Society, Providence, RI, 2018, 143–195.Google Scholar
Kobayashi, S., Negative vector bundles and complex Finsler structures , Nagoya Math. J. 57 (1975), 153–166.Google Scholar
Kobayashi, S., Differential Geometry of Complex Vector Bundles, Publications of the Mathematical Society of Japan, 15, Princeton University Press, Princeton, NJ, 1987, Kanô Memorial Lectures, 5.Google Scholar
Kobayashi, S., “Complex Finsler vector bundles” in Finsler Geometry (Seattle, WA, 1995), Contemp. Math., 196, American Mathematical Society, Providence, RI, 1996, 145–153.CrossRefGoogle Scholar
Lempert, L., A maximum principle for Hermitian (and other) metrics , Proc. Amer. Math. Soc. 143 (2015), 2193–2200.CrossRefGoogle Scholar
Lempert, L., “Extrapolation, a technique to estimate” in Functional Analysis, Harmonic Analysis, and Image Processing: A Collection of Papers in Honor of Björn Jawerth, Contemp. Math., 693, American Mathematical Society, Providence, RI, 2017, 271–281.Google Scholar
Liu, K., Sun, X., and Yang, X., Positivity and vanishing theorems for ample vector bundles, J. Algebraic Geom. 22 (2013), 303–331.CrossRefGoogle Scholar
Liu, K. and Yang, X., Curvatures of direct image sheaves of vector bundles and applications , J. Diff. Geom. 98 (2014), 117–145.Google Scholar
Mourougane, C. and Takayama, S., Hodge metrics and positivity of direct images, J. Reine Angew. Math. 606 (2007), 167–178.Google Scholar
Mourougane, C. and Takayama, S., Hodge metrics and the curvature of higher direct images , Ann. Sci. Éc. Norm. Supér. (4) 41 (2008), 905–924.CrossRefGoogle Scholar
Naumann, P., An approach to Griffiths conjecture, preprint, arXiv:1710.10034 Google Scholar
Pingali, V. P., A note on Demailly’s approach towards a conjecture of Griffiths, preprint, arxiv:2102.02496 Google Scholar
Rochberg, R., Interpolation of Banach spaces and negatively curved vector bundles , Pacific J. Math. 110 (1984), 355–376.CrossRefGoogle Scholar
Sommese, A. J., Concavity theorems , Math. Ann. 235 (1978), 37–53.CrossRefGoogle Scholar
Umemura, H., Some results in the theory of vector bundles , Nagoya Math. J. 52 (1973), 97–128.Google Scholar
Zhou, X. and Zhu, L., An optimal $\ {L}^2\ {}$ extension theorem on weakly pseudoconvex Kähler manifolds , J. Differ. Geom. 110 (2018), 135–186.Google Scholar