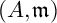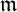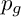NORMAL HILBERT COEFFICIENTS AND ELLIPTIC IDEALS IN NORMAL TWO-DIMENSIONAL SINGULARITIES

Abstract

Let $(A,\mathfrak m)$ be an excellent two-dimensional normal local domain. In this paper, we study the elliptic and the strongly elliptic ideals of A with the aim to characterize elliptic and strongly elliptic singularities, according to the definitions given by Wagreich and Yau. In analogy with the rational singularities, in the main result, we characterize a strongly elliptic singularity in terms of the normal Hilbert coefficients of the integrally closed $\mathfrak m$ -primary ideals of A. Unlike $p_g$ -ideals, elliptic ideals and strongly elliptic ideals are not necessarily normal and necessary, and sufficient conditions for being normal are given. In the last section, we discuss the existence (and the effective construction) of strongly elliptic ideals in any two-dimensional normal local ring.

1 Introduction and notations

Let $(A,\mathfrak m)$ be an excellent two-dimensional normal local ring, and let I be an $\mathfrak m$ -primary ideal of A. The integral closure $\bar {I}$ of I is the ideal consisting of all solutions z of some equation with coefficients $c_i \in I^i $ : $Z ^n +c_1 Z^{n-1} +c_2 Z^{n-2} + \dots + c_{n-1} Z + c_n=0$ . Then $ I \subseteq \bar {I} \subseteq \sqrt {I}$ . We say that I is integrally closed if $I = \bar {I}$ and I is normal if $I^n= {\overline {I^n}} $ for every positive integer n. By a classical result of Rees [29], under our assumptions, the filtration $\{\overline {I^n}\}_{n \in \mathbb N}$ is a good I-filtration of A and it is called the normal filtration.

We may define the Hilbert–Samuel function $\bar {H}_I(n):=\ell _A(A/\overline {I^{n+1}})$ for all integers $n \ge 0$ , and it becomes a polynomial for large n. (Here, $\ell _A(M) $ is the length of the A-module M.) This polynomial is called the normal Hilbert polynomial

$$ \begin{align*} \bar{P}_I(n) =\bar e_0(I) \binom{n+2}{2} -\bar e_1(I) \binom{n+1}{1} +\bar e_2(I), \end{align*} $$

and the coefficients $\overline {e}_i(I)$ , $i=0,1,2,$ are the normal Hilbert coefficients.

A rich literature is available on the normal Hilbert coefficients $\bar e_i(I)$ , and this study is considered an important part of the theory of blowing-up rings (see, e.g., [2], [3], [10], [11], [12], [17]–[19], [33]).

From the geometric side, any integrally closed $\mathfrak m$ -primary ideal I of $A $ is represented on some resolution (see [16]). Let

$$ \begin{align*}f \colon X \to \operatorname{\mathrm{Spec}} A\end{align*} $$

be a resolution of singularities with an anti-nef cycle $Z>0$ on X, so that $I =I_Z= H^0(\mathcal {O}_X(-Z))$ and $I\mathcal {O}_X=\mathcal {O}_X(-Z)$ . We say that $I = I_Z$ is represented by $Z $ on X. The aim of this paper is to join the algebraic and the geometric information on A taking advantage of the theory of the Hilbert functions and of the theory of the resolution of singularities.

For a coherent $\mathcal {O}_X$ -module $\mathcal {F}$ , we write $h^i(\mathcal {F})=\ell _A(H^i(X, \mathcal {F}))$ . If $I=I_Z$ is an $\mathfrak m$ -primary integrally closed ideal of A represented by Z on X, one can define for every integer $n \ge 0$ a decreasing chain of integers $q(nI):= q(\overline {I^n}) = h^1(\mathcal {O}_X(-nZ))$ where $q(0I) := p_g(A)$ is the geometric genus of A. It is proved that $q(nI) $ stabilizes for every I and $n\ge p_g(A)$ . We denote it by $q(\infty I)$ .

These integers are independent of the representation, and they are strictly related to the normal Hilbert polynomial. The keys of our approach can be considered Theorem 2.2 and Proposition 2.6, consequences of Kato’s Riemann–Roch formula (see [14], [24]). In particular, the following holds:

1. (1) $\overline {P}_I(n)=\ell _A(A/\overline {I^{n+1}})$ for all $n \ge p_g(A)-1$ .

2. (2) $\bar e_1(I)-e_0(I) + \ell _A(A/I) =p_g(A) - q(I)$ .

3. (3) $\bar e_2(I)= p_g(A)-q(nI)=p_g(A)-q(\infty I)$ for all $n \ge p_g(A)$ .

Moreover, we have

$$ \begin{align*} \bar e_0(I)= -Z^2,\qquad \bar e_1(I)= \dfrac{-Z^2+ZK_X}{2}. \end{align*} $$

This makes the bridge between the theory of the normal Hilbert coefficients and the theory of the singularities. This is the line already traced by Lipman [16], Cutkosky [4], and more recently by Okuma, Watanabe, and Yoshida (see [23]–[25]).

Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain containing an algebraically closed field $k= A/\mathfrak m$ . It is known that A is a rational singularity (see [1]) if and only if every integrally closed $\mathfrak m$ -primary ideal I of A is normal (see [4], [16]), equivalently $\bar e_2(I)=0$ , that is, I is a $p_g$ -ideal, as proved in [23], [24]. Inspired by a paper by Okuma [22], we investigate the integrally closed $\mathfrak m$ -primary ideals of elliptic singularities (see [38]) and of strongly elliptic singularities (see [41]). All the preliminary results are contained in §2.

In §3, we prove the main results of the paper. We define the elliptic and the strongly elliptic ideals aimed by the study of nonrational singularities. We recall that if Q is a minimal reduction of I, then we denote by $\bar {\mathrm {r}}(I):= \min \{ r \;|\; \overline {I^{n+1}} = Q \overline {I^n}\;, \text {for all} \; n \ge r\}$ , the normal reduction number of I and this integer exists and does not depend on the choice of Q. Okuma proved that if A is an elliptic singularity, then $\bar {\mathrm {r}}(I) = 2$ for any integrally closed $\mathfrak m$ -primary ideal of A (see [22, Theorem 3.3]). According to Okuma’s result, we define elliptic ideals to be the integrally closed $\mathfrak m$ -primary ideals satisfying $\bar {\mathrm {r}}(I)= 2$ . In Theorem 3.2, we prove that elliptic ideals satisfy $\bar e_2(I)=\bar {e}_1(I) -e_0(I) + \ell _A( A/I)>0 $ attaining the minimal value according to the inequality proved by Sally [35] and Itoh [12]. In particular, if I is an elliptic ideal, then $p_g(A)> q(I)=q(\infty I)$ . If A is not a rational singularity, then elliptic ideals always exist (see Proposition 3.3). In particular, we prove the following proposition.

Proposition 1.1 (See Proposition 3.3)

If A is not a rational singularity, then for any $\mathfrak m$ -primary integrally closed ideal I of A, $\overline {I^{n}}$ is either a $p_g$ -ideal or an elliptic ideal for every $n \ge p_g(A)$ .

Yau in [41], Laufer in [15], and Wagreich in [38] introduced interesting classes of elliptic singularities. An excellent two-dimensional normal local ring A is a strongly elliptic singularity if $ p_g(A)=1$ , that is, $p_g$ is almost minimal.

Among the elliptic ideals, in Theorem 3.9, we define strongly elliptic ideals those for which $\bar e_2 =1 $ and equivalent conditions are given. The following result characterizes algebraically the strongly elliptic singularities.

Theorem 1.2 (See Theorem 3.14)

Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain containing an algebraically closed field $k= A/\mathfrak m$ , and assume that $p_g(A)>0$ . The following conditions are equivalent $:$

1. (1) A is a strongly elliptic singularity.

2. (2) Every integrally closed ideal of A is either a $p_g$ -ideal or a strongly elliptic ideal.

Notice that $p_g$ -ideals are always normal, but elliptic ideals are not necessary normal (see Proposition 3.16 and Examples 3.15 and 3.25). Moreover, if A is strongly elliptic and I is not a $p_g$ -ideal, then Proposition 3.16 and Theorem 3.23 give necessary and sufficient conditions for being I normal.

Theorem 1.3. Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain containing an algebraically closed field $k= A/\mathfrak m$ . Assume that A is a strongly elliptic singularity. If $I = I_Z $ is an elliptic ideal $($ equivalently, I is not a $p_g$ -ideal $)$ and D is the minimally elliptic cycle on X, then $I^2$ is integrally closed $($ equivalently, I is normal $)$ if and only if $- Z D \ge 3$ and if $- ZD \le 2$ , then $I^2 = QI$ .

For any normal surface singularity which is not rational, $p_g$ -ideals and elliptic ideals exist plentifully. But this is no longer true for strongly elliptic ideals.

In §4, we show that there exist excellent two-dimensional normal local rings having no strongly elliptic ideals (see Example 4.8). Finally, Corollary 4.7 gives necessary and sufficient conditions for the existence of strongly elliptic ideals in terms of the existence of certain cohomological cycles. When there exist, we present an effective geometric construction (see Example 4.9).

2 Preliminaries and normal reduction number

Let $(A,\mathfrak m)$ be an excellent two-dimensional normal local domain containing an algebraically closed field $k= A/\mathfrak m$ , and let I be an integrally closed $\mathfrak m$ -primary ideal of A. With the already introduced notation, then there exists a resolution $X \to \ \operatorname {\mathrm {Spec}} A$ and a cycle Z such that I is represented on X by Z. When we write $I_Z$ , we always assume that $\mathcal {O}_X(-Z) $ is generated by global sections, namely $I \mathcal {O}_X=\mathcal {O}_X(-Z)$ , and note that $I_Z= H^0(X, \mathcal {O}_X(-Z))$ . Recall that the geometric genus $p_g(A)= h^1(\mathcal {O}_X)$ is independent of the choice of the resolution.

Okuma, Watanabe, and Yoshida introduced a natural extension of the integrally closed ideals in a two-dimensional rational singularity, that is, the $p_g$ -ideals. With the previous notation,

$$ \begin{align*} p_g(A) \ge h^1(\mathcal{O}_X(-Z) ), \end{align*} $$

and if the equality holds, then Z is called a $p_g$ -cycle and $I=I_Z$ is called a $p_g$ -ideal. In [23], [24], the authors characterized the $p_g$ -ideals in terms of the normal Hilbert polynomial. They proved that A is a rational singularity if and only if every integrally closed $\mathfrak m$ -primary ideal is a $p_g$ -ideal. Starting by $p_g(A)$ , we define the following chain of integers.

Definition 2.1. We define $q(I):= h^1(\mathcal {O}_X(-Z))$ and more in general $q(nI):= q(\overline {I^n}) = h^1(\mathcal {O}_X(-nZ))$ for every integer $n \ge 1$ .

We put $q(0 I)=h^1(\mathcal {O}_X)=p_g(A)$ . Notice that $q(nI)$ is in general very difficult to compute, but it is independent of the representation (see [23, Lemma 3.4]). These invariants are strictly related to the normal Hilbert polynomial, and their interplay is very important in our approach.

The following formula is called a Riemann–Roch formula. The result was proved in [14] in the complex case, but it holds in any characteristic (see [40]).

Theorem 2.2 (Kato’s Riemann–Roch formula [40, Theorem 2.2])

Let $I=I_Z$ be an $\mathfrak m$ -primary integrally closed ideal represented by an anti-nef cycle Z on X. Then we have

$$ \begin{align*} \ell_A(A/I) + q(I) =-\dfrac{Z^2+K_XZ}{2} + p_g(A), \end{align*} $$

where $K_X$ denotes the canonical divisor.

We recall here the properties of the sequence $\{q(nI)\}$ . Propositions 2.3 and 2.5 on $I = I_Z$ follow from the long exact sequence attached to the short exact sequence

$$ \begin{align*} (\dagger) \quad 0\to \mathcal{O}_X(-(n-1)Z) \to \mathcal{O}_X(-nZ)^{\oplus 2}\to \mathcal{O}_X(-(n+1)Z)\to 0 \end{align*} $$

(see [24, Lemma 3.1]).

Proposition 2.3. With the previous notation, the following facts hold $:$

1. (1) $0 \le q(I) \le p_g(A)$ .

2. (2) $q(kI) \ge q((k+1)I)$ for every integer $k \ge 0$ and if $q(nI) = q((n+1)I)$ for some $n\ge 0$ , then $q(nI) = q(mI)$ for every $m\ge n$ . Hence, $q(nI) = q((n+1)I)$ for every I and $n\ge p_g(A)$ . We denote it by $q(\infty I)$ .

We use the above sequence for computing the following important algebraic numerical invariants of the normal filtration $\{\overline {I^n}\}$ . Let $\mathbb {Z}_{+}$ denote the set of positive integers.

Definition 2.4 (cf. [26])

Let $I \subset A$ be $\mathfrak m$ -primary integrally closed ideal, and let Q be a minimal reduction of I. Define:

$$ \begin{align*} \operatorname{\mathrm{nr}}(I) &:= \min\{r \in \mathbb{Z}_{+} \,|\, \overline{I^{r+1}}=Q\overline{I^r}\}, \\ \bar{\mathrm{r}}(I) &:= \min\{ r \in \mathbb{Z}_{+} \;|\; \overline{I^{n+1}} = Q \overline{I^n} \; \mbox{for all } n \ge r\}. \end{align*} $$

We call $\bar {\mathrm {r}}(I)$ the normal reduction number and $\operatorname {\mathrm {nr}}(I)$ the relative normal reduction number.

The normal reduction number exists (see [21], [29]), and it has been studied by many authors in the context of the Hilbert function and of the Hilbert polynomial (see, e.g., [2], [3], [10], [12], [19]). The main difficulty of the normal filtration with respect to the I-adic filtration is that the Rees algebra of the normal filtration is not generated by the part of degree one because $I \overline {I^n} \neq \overline {I^{n+1}}$ . By the definition, we deduce that $\operatorname {\mathrm {nr}}(I) \le \bar {\mathrm {r}}(I)$ and we see that, in general, they do not coincide. Note that the definitions of $\operatorname {\mathrm {nr}}(I)$ and of $\bar {\mathrm {r}}(I)$ are independent on the choice of a minimal reduction Q of I (see, e.g., [10, Theorem 4.5]). It is also a consequence of the following result in [26, §2].

Proposition 2.5. The following statements hold.

1. (1) For any integer $n \ge 1$ , we have

   $$ \begin{align*} 2 \cdot q(nI) + \ell_A(\overline{I^{n+1}}/Q\overline{I^n}) =q((n+1)I)+q((n-1)I). \end{align*} $$

2. (2) We have

   $$ \begin{align*} \operatorname{\mathrm{nr}}(I) &= \min\{n \in \mathbb{Z}_{+} \,| \, q((n-1)I)- q(nI) = q(nI) - q((n+1)I) \},\\[6pt] \bar{\mathrm{r}}(I) &= \min\{n \in \mathbb{Z}_{+} \,|\, q((n-1)I)=q(nI) \}. \end{align*} $$

From the propositions above, we have that $\bar {\mathrm {r}}(I) \le p_g(A) +1$ . In [26, Theorem 2.9], the authors showed that $p_g(A) \ge \binom {\operatorname {\mathrm {nr}}(I)}{2}$ .

Rossi [32, Corollary 1.5] proved the following upper bound on the reduction number $r(I)$ for every $\mathfrak m$ -primary ideal I (here, $r(I)$ denotes the reduction number for the I-adic filtration) in a two-dimensional Cohen–Macaulay local ring A in terms of the Hilbert coefficients:

$$ \begin{align*} r(I) \le e_1(I) -e_0(I) + \ell_A(A/I)+1. \end{align*} $$

The bound gives, as a consequence, several interesting results, in particular a positive answer to a long-standing conjecture stated by Sally in the case of local Cohen–Macaulay rings of almost minimal multiplicity (see [32], [34]). Later, the inequality was extended by Rossi and Valla (see [33, Theorem 4.3] for special multiplicative I-filtrations). The result does not include the normal filtration. It is natural to ask if the same bound also holds for $\bar {\mathrm {r}}(I)$ . The answer is negative as we will show later, but we prove that the analogue upper bound holds true for $\operatorname {\mathrm {nr}}(I)$ . We need some preliminary results.

From Riemann–Roch formula (Theorem 2.2), we get

$$ \begin{align*} \ell_A(A/\overline{I^{n+1}})+q((n+1)I) =-\dfrac{(n+1)^2Z^2+(n+1)ZK_X}{2} + p_g(A). \end{align*} $$

Using this, we can express $\bar {e}_0(I), \bar {e}_1(I), \bar {e}_2(I)$ as follows.

Proposition 2.6 [24, Theorem 3.2]

Assume that $I = I_Z$ is represented by a cycle $Z> 0$ on a resolution X of $\operatorname {\mathrm {Spec}}(A)$ . Let $\bar {P}_I(n)$ be the normal Hilbert polynomial of I. Then $:$

1. (1) $\overline {P}_I(n)=\ell _A(A/\overline {I^{n+1}})$ for all $n \ge p_g(A)-1$ .

2. (2) $\bar e_0(I)=e_0(I)$ .

3. (3) $\bar e_1(I)-e_0(I) + \ell _A(A/I) =p_g(A) - q(I)$ .

4. (4) $\bar e_2(I)= p_g(A)-q(nI)=p_g(A)-q(\infty I)$ for all $n \ge p_g(A)$ .

Moreover, we have

$$ \begin{align*} \bar e_0(I)= -Z^2,\qquad \bar e_1(I)= \dfrac{-Z^2+ZK_X}{2}. \end{align*} $$

Theorem 2.7. Let $(A,\mathfrak m)$ be an excellent two-dimensional normal local domain containing an algebraically closed field $k= A/\mathfrak m$ . Let $I \subset A$ be an $\mathfrak m$ -primary integrally closed ideal. Then

$$ \begin{align*} \operatorname{\mathrm{nr}}(I) \le \bar{e}_1(I) - \bar{e}_0(I) +\ell_A(A/I) +1. \end{align*} $$

If we put $r=\operatorname {\mathrm {nr}}(I)$ , equality holds if and only if the following conditions hold true $:$

1. (1) $\ell _A(\overline {I^{n+1}}/Q\overline {I^n}) =1$ for $n= 1,\ldots , r-1$ if $r>1,$

2. (2) $q((r-1)I)=q(\infty I)$ .

When this is the case, $\operatorname {\mathrm {nr}}(I)=\bar {\mathrm {r}}(I)$ , $q(I)=p_g(A)-\bar {\mathrm {r}}(I)+1$ , and $\bar {e}_2(I)=p_g(A)- q(\infty I) = r(r-1)/2$ .

Proof. By virtue of Proposition 2.6, it is enough to show

$$ \begin{align*} \operatorname{\mathrm{nr}}(I) \le p_g(A)-q(I)+1. \end{align*} $$

If we put $\Delta q(n) : = q(nI) - q((n+1)I)$ for every integer $n \ge 0$ , then $\Delta q(n) $ is nonnegative and decreasing since $\ell _A(\overline {I^{n+1}}/Q\overline {I^n}) =\Delta q(n-1) -\Delta q(n)$ . We have

$$ \begin{align*} \operatorname{\mathrm{nr}}(I)=\min\{n \in \mathbb{Z}_{+} \,|\, \Delta q(n-1) =\Delta q(n) \}, \quad \bar{\mathrm{r}}(I)=\min\{n \in \mathbb{Z}_{+} \,|\, \Delta q(n-1) =0 \}. \end{align*} $$

Put $a=p_g(A)-q(I)$ . Then $\Delta q(0)=a\ge \operatorname {\mathrm {nr}}(I)-1$ and $\operatorname {\mathrm {nr}}(I)=a+1$ if and only if

$$ \begin{align*} \Delta q(0) =a> \Delta q(1) =a-1 > \cdots > \Delta q(a-1)=1 > \Delta q(a)=0 = \Delta q(a+1). \end{align*} $$

Now, assume $\operatorname {\mathrm {nr}}(I)=a+1$ . Then $a=r-1$ and for every n with $1 \le n \le a=r-1$ , we have

$$ \begin{align*} \ell_A(\overline{I^{n+1}}/Q\overline{I^n})=\Delta q(n-1)-\Delta q(n)= (a-n+1)-(a-n)=1. \end{align*} $$

Moreover, for every $n \ge a+1$ , we have

$$ \begin{align*} \ell_A(\overline{I^{n+1}}/Q\overline{I^n})=\Delta q(n-1)-\Delta q(n)=0, \end{align*} $$

and thus $\overline {I^{n+1}}=Q\overline {I^n}$ . Hence, $\bar {\mathrm {r}}(I)=a+1=\operatorname {\mathrm {nr}}(I)$ . Furthermore,

$$ \begin{align*} \bar{e}_2(I)=p_g(A)-q(\infty I)=q(0 I)-q((r-1)I) = \sum_{i=0}^{r-2} \Delta q(i)= \dfrac{r(r-1)}{2}. \end{align*} $$

One can prove the converse similarly.

Note that, if the equality holds in the previous result, then the normal filtration $\{\overline {I^n}\} $ has almost minimal multiplicity following the definition given in [33, 2.1]. In the following example, we show that Theorem 2.7 does not hold if we replace $\operatorname {\mathrm {nr}}(I)$ by $\bar {r}(I)$ . The example shows that for all $g \ge 2$ , there exist an excellent two-dimensional normal local ring A and an integrally closed $\mathfrak m$ -primary ideal I such that $\operatorname {\mathrm {nr}}(I) =1, \bar {r}(I)={{g+1}}, q(I) = g-1$ and $\ell _A(A/I) = g$ .

The following ideal I satisfies $\bar {e}_1(I)=\bar {e}_0(I)-\ell _A(A/I)+1$ , but $\bar {\mathrm {r}}(I)\not \le 2$ .

Example 2.8 [27, Example 3.10]

Let $g \ge 2$ be an integer, and let K be a field of $\operatorname {\mathrm {char}} K=0$ or $\operatorname {\mathrm {char}} K=p$ , where p does not divide $2g+2$ . Then $R=K[X,Y,Z]/(X^2-Y^{2g+2}-Z^{2g+2})$ is a graded normal K-algebra with $\deg X=g+1$ , $\deg Y=\deg Z=1$ . Let $A=R^{(g)}$ be the gth Veronese subring of R:

$$ \begin{align*} A=K[y^{g},y^{g-1}z,y^{g-2}z^{2},\ldots, z^{g}, xy^{g-1},xy^{g-2}z, \ldots,xz^{g-1}], \end{align*} $$

where $x, y, z$ denote, respectively, the image of $X, Y, Z$ in R. Then A is a graded normal domain with $A_k=R_{kg}$ for every integer $k \ge 0$ . Let $I=(y^g,y^{g-1}z) +A_{\ge 2}$ and $Q=(y^g-z^{2g}, y^{g-1}z)$ . Then the following statements hold:

1. (1) $p_g(A)=g$ .

2. (2) $\operatorname {\mathrm {nr}}(I)=1$ and $\bar {\mathrm {r}}(I)=g+1$ . Indeed,

   1. (a) $\overline {I}=I$ and $\overline {I^{n}}=I^n=QI^{n-1}$ for every $n=2,\ldots , g$ .

   2. (b) $\ell _A(\overline {I^{g+1}}/Q\overline {I^g})=1$ ( $\overline {I^{g+1}}= I^{g+1} +(xy^{g^2-1})$ ).

   3. (c) $\overline {I^{n+1}}=Q \overline {I^{n}}$ for every $n \ge g+1$ .

3. (3) $\bar {e}_0(I)=4g-2$ , $\bar {e}_1(I)=3g-1$ , $\bar {e}_2(I)=g$ , and $\ell _A(A/I)=g$ .

4. (4) $q(nI)=g-n$ for every $n=0,1,\ldots ,g$ ; $q(gI)=q(\infty I)=0$ .

The first statement follows from that $a(A)=0$ and $g=g(\operatorname {\mathrm {Proj}} (A))$ . For the convenience of the readers, we give a sketch of the proof in the case of $g=2$ (see [27, Proof of Example 3.10]). Let $A=K[y^2,yz,z^2,xy,xz]=R^{(2)}$ with $\deg x=3$ and $\deg y= \deg z=1$ , and $I=(y^2,yz, z^4, xy,xz) \supset Q=(y^2-z^4,yz)$ . Then one can easily see that $e_0(I)=\ell _A(A/Q)=4g-2=6$ , $\ell _A(A/I)=p_g(A)=g=2$ , and $I^2=QI$ , $\overline {I}=I$ . In particular, $\operatorname {\mathrm {nr}}(I)=1$ .

Claim 1. $f_0 \in K[y,z]_{2n} \cap \overline {I^n} \Longrightarrow f_0 \in I^n$ for each $n \ge 1$ .

The normality of $I_0=(y^2,yz,z^4)K[y,z] \subset K[y,z]$ implies the above claim.

Claim 2. $0 \ne f_1 \in K[y,z]_{2n-3}$ , $xf_1 \in \overline {I^n} \Longrightarrow n \ge 3$ .

By assumption and Claim 1, we have $(y^6+z^6)f_1^2=(xf_1)^2 \in \overline {I^{2n}} \cap K[y,z]_{2 \cdot 2n} \subset I^{2n}$ . The degree (in y and z) of any monomial in $I^{2n}=(y^2, yz, z^4, xy, xz)$ is at least $4n=\deg (y^6+z^6) f_1^2$ . Hence, $(y^6+z^6)f_1^2 \in (y^2, yz)^{2n}$ , and the highest power of z appearing in $(y^6+z^6) f_1^2$ is at most $2n$ . Therefore, $n \ge 3$ .

Claim 3. If $n \le 2$ , then $\overline {I^n} \cap A_n \subset I^n \cap A_n$ .

Any $f \in \overline {I^n} \cap A_n$ can be written as $f=f_0+xf_1$ for some $f_0 \in K[y,z]_{2n}$ and $f_1 \in K[y,z]_{2n-3})$ . Let $\sigma \in \operatorname {\mathrm {Aut}}_{K[y,z]^{(2)}}(A)$ such that $\sigma (x)=-x$ . Then, since $\sigma (I)=I$ , we obtain $\sigma (f)=f_0 - xf_1 \in \overline {I^n}$ . Hence,

$$ \begin{align*} f_0 = \frac{f+\sigma(f)}{2} \in \overline{I^n} \quad \text{and} \quad xf_1 =\frac{f-\sigma(f)}{2} \in \overline{I^n}. \end{align*} $$

By Claims 1 and 2, we have $f_0 \in I^n$ and $f_1=0$ . Therefore, $f=f_0 \in I^n \cap A_n$ , as required.

Claim 4. $xy^3 \in \overline {I^3} \setminus Q\overline {I^2}$ .

Since $(xy^3)^2=(y^6)^2+(y^3z^3)^2 \in (I^3)^2$ , we get $xy^3 \in \overline {I^3}$ . Assume $xy^3 \in Q\overline {I^2}=(a,b)\overline {I^2}$ , where $a=y^2-z^4$ and $b=yz$ . Then $axy+bxz^3=xy^3=au+bv$ for some $u,v \in \overline {I^2}$ . Since $a,b$ form a regular sequence, we can take an element $h \in A_1$ , so that $u-xy=bh$ and $xz^3-v =ah$ . So we may assume $u,v \in A_2$ , and thus $u,v \in \overline {I^2} \cap A_2 \subset I^2$ . However, this yields $xy^3=au+bv \in QI^2=I^3$ , which is a contradiction.

Claim 5. $q(I)=1$ , $q(2I)=q(\infty I)=0$ , $\ell _A(\overline {I^3}/Q\overline {I^2})=1$ , and $\overline {I^{n+1}}=Q\overline {I^n}$ for each $n \ge 3$ .

By Proposition 2.3, we have $2=p_g(A)=q(0\cdot I)\ge q(I) \ge q(2\cdot I) \ge 0$ . If $q(I)=q(2\cdot I)$ , then $q(2 \cdot I)=q(3 \cdot I)$ . This implies $\ell _A(\overline {I^3}/Q\overline {I^2})=0$ from Proposition 2.5. This contradicts Claim 4. Hence, $q(I)=1$ and $q(2\cdot I)=0$ . The other assertions follow from Proposition 2.5. In particular, $\bar {\mathrm {r}}(I)=3$ .

Claim 6. $\bar{e_1}(I)=3g-2=5$ and $\bar{e_2}(I)=g=2$ .

By Proposition 2.6, we have

$$ \begin{align*} \bar e_1(I)&= e_0(I)-\ell_A(A/I)+p_g(A)-q(I)=6-2+2-1=5, \\ \bar e_2(I) &= p_g(A)-q(\infty I)=~2-0=2. \end{align*} $$

3 Elliptic and strongly elliptic ideals

We define the Rees algebra $\bar {\mathcal R}(I)$ and the associated graded ring $\bar {G}(I)$ associated with the normal filtration as follows:

$$ \begin{align*} \bar{\mathcal R}(I) &:= \bigoplus_{n\ge 0}\overline{I^n} t^n \subset A[t]. \\ \bar{G}(I) &:= \bigoplus_{n\ge 0}\overline{I^n}/ \overline{I^{n+1}} \cong \bar{\mathcal R}(I)/\bar{\mathcal R}(I)(1). \end{align*} $$

$\bar {\mathcal R}(I)$ (resp. $\bar {G}(I)$ ) is called the normal Rees algebra (resp. the normal associated graded ring) of I. We recall that the a-invariant of a graded d-dimensional ring R with maximal homogeneous graded ideal $\mathfrak {M}$ was introduced by Goto and Watanabe [9] and defined as $a(R):= \max \{n | [H^d_{\mathfrak M}(R)]_n \neq 0\}$ , where $[H^d_{\mathfrak M}(R) ]_n$ denotes the homogeneous component of degree n of the graded R-module $H^d_{\mathfrak M}(R)$ .

It is known that A is a rational singularity if and only if $\overline r(A)=1$ (see [27, Proposition 1.1]). In [23], [24], the authors introduced the notion of $p_g$ -ideals, characterizing rational singularities.

Theorem 3.1 (cf. [7], [10], [23], [24])

Let $(A,\mathfrak m)$ be a two-dimensional excellent normal nonregular local domain containing an algebraically closed field $k= A/\mathfrak m. $ Let $I=I_Z$ be an $\mathfrak m$ -primary integrally closed ideal of A. Put $\bar {G}=\bar {G}(I)$ and $\bar {\mathcal R}=\bar {\mathcal R}(I)$ . Then the following conditions are equivalent $:$

1. (1) $\bar {\mathrm {r}}(I)= 1$ .

2. (2) $q(I)=p_g(A)$ .

3. (3) $I^2=QI$ and $\overline {I^n}=I^n$ for every $n \ge 1$ .

4. (4) $\bar e_1(I) = e_0(I)-\ell _A(A/I)$ .

5. (5) $\bar e_2(I)=0$ .

6. (6) $\bar {G}$ is Cohen–Macaulay with $a(\bar {G})< 0$ .

7. (7) $\bar {\mathcal R}$ is Cohen–Macaulay.

When this is the case, I is said to be a $p_g$ -ideal.

Proof. Since $QI^{n-1} \subset I^n \subset \overline {I^n}$ for every $n \ge 2$ , (1) $\Leftrightarrow (3)$ is trivial. (1) $\Leftrightarrow $ (5) (resp. (6) $\Leftrightarrow $ (7)) follows from [7, Part II, Proposition 8.1] (resp. [7, Part II, Corollary 1.2]). Moreover, the equivalence of (4), (5), and (7) follows from [7, Part II, Theorem 8.2]. (2) $\Leftrightarrow $ (4) follows from Proposition 2.5.

It is known that A is a rational singularity if and only if any integrally closed $\mathfrak m$ -primary ideal is a $p_g$ -ideal (see [23], [24]). We define

$$ \begin{align*} \overline{r}(A):=\max\{\bar{\mathrm{r}}(I) \,|\, I\ \text{is an integrally closed}\ \mathfrak m\text{-primary ideal}\}. \end{align*} $$

Then A is a rational singularity if and only if $\overline r(A)=1$ (see [27, Proposition 1.1]).

Okuma proved in [22, Theorem 3.3] that if A is an elliptic singularity, then $\overline r(A)=2$ . For the definition of elliptic singularity, we refer to [38, p. 428] or [22, Definition 2.1]. We investigate the integrally closed $\mathfrak m$ -primary ideals such that $\bar {\mathrm {r}}(I) =2$ with the aim to characterize elliptic singularities. Next result extends and completes a result by Itoh [12, Proposition 10], by using a different approach.

Theorem 3.2. Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain containing an algebraically closed field $k= A/\mathfrak m$ , and let $I \subset A$ be an $\mathfrak m$ -primary integrally closed ideal. Put $\bar {G}=\bar {G}(I)$ and $\bar {\mathcal R}=\bar {\mathcal R}(I)$ . Then the following conditions are equivalent $:$

1. (1) $\bar {\mathrm {r}}(I)=2$ .

2. (2) $p_g(A)> q(I)=q(\infty I)$ .

3. (3) $\bar {e}_1(I) = e_0(I) -\ell _A( A/I) + \bar {e}_2(I)$ and $\bar {e}_2(I)>0$ .

4. (4) $\ell _A(A/\overline {I^{n+1}}) = \bar {P}_I(n)$ for all $n\ge 0$ and $\bar {e}_2(I)>0$ .

5. (5) $\bar {G}$ is Cohen–Macaulay with $a(\bar {G})=0$ .

When this is the case, I is said to be an elliptic ideal and $\ell _A ([H^2_{\mathfrak M}(\bar {G})_0) = \ell _A(\overline {I^2}/QI) = \bar {e}_2(I)$ .

Proof. $(1) \Longleftrightarrow (2):$ It follows from Proposition 2.5(2).

$(2) \Longleftrightarrow (3):$ By Proposition 2.6, we have

$$ \begin{align*} \bar{e}_1(I) &= e_0(I) -\ell_A( A/I) + \bar{e}_2(I) - \big\{q(I)-q(\infty I)\big\}. \\ \bar{e}_2(I) &= p_g(A) - q(\infty I) \ge 0. \end{align*} $$

The assertion follows from here.

$(2) \Longleftrightarrow (4):$ Assume $I= I_Z = H^0(X,\mathcal {O}_X(-Z))$ for some resolution $X \to \operatorname {\mathrm {Spec}} A$ . By Kato’s Riemann–Roch formula, for every integer $n \ge 0$ , we have

$$ \begin{align*} \ell_A(A/\overline{I^{n+1}})+h^1(\mathcal{O}_X(-(n+1)Z)) =-\dfrac{(n+1)^2Z^2+(n+1) K_XZ}{2} +p_g(A). \end{align*} $$

Hence,

$$ \begin{align*} \ell_A(A/\overline{I^{n+1}}) &= \bar{e}_0(I){n+2 \choose 2} - \bar{e}_1(I) {n+1 \choose 1} + \big\{p_g(A)-q((n+1)I) \big\} \\ &= \bar{P}_I(n)- \big\{q((n+1)I)-q(\infty I) \big\}. \end{align*} $$

Assume (4). By replacing $0$ to n in the above equation, we get $q(I)=q(\infty I)$ , hence (2). Conversely, if $q(I)=q(\infty I)$ , then since $q((n+1)I)=q(\infty I)$ for all $n \ge 1$ , the above equation implies (4).

$(1) \Longrightarrow (5):$ Put $Q=(a,b)$ . Since $\overline {I^{n+1}} \colon a=\overline {I^n}$ , $a^{*}$ , the image of a in $\bar {G}$ is a nonzero divisor of $\bar {G}$ .

By assumption, we have $\overline {I^{n+1} } \cap Q = Q {\overline {I^{n}}} \cap Q =Q {\overline {I^{n}}}$ for every $n \ge 2$ . On the other hand, we have $\overline {I^2} \cap Q = QI$ by [10, Theorem in p. 371] or [11, Theorem]. Then it is well known that $a^{*}$ , $b^{*}$ form a regular sequence in $\bar {G}$ , and thus $\bar {G}$ is Cohen–Macaulay (see also [37]) and $2=\bar {\mathrm {r}}(I)=a(\bar {G})+\dim A=a(\bar {G})+2$ . Thus, $a(\bar {G})=0$ , as required.

$(5) \Longrightarrow (1):$ Since $\bar {G}$ is Cohen–Macaulay, we have $\bar {\mathrm {r}}(I)=a(\bar {G})+\dim A=0+2=2$ .

We notice that if A is not a rational singularity, then elliptic ideals always exist.

Proposition 3.3. Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain containing an algebraically closed field $k= A/\mathfrak m$ , and let $I \subset A$ be an $\mathfrak m$ -primary integrally closed ideal which is not a $p_g$ -ideal. Then there exists a positive integer n such that $\overline {I^n} $ is an elliptic ideal. In particular, if A is not a rational singularity, then for any $\mathfrak m$ -primary integrally closed ideal I of A, then $\overline {I^{n}}$ is either a $p_g$ -ideal or an elliptic ideal for every $n \ge p_g(A)$ .

Proof. Let n be a positive integer such that $\ell _A(A/\overline {I^{n}})=\bar {P}_I(n-1)$ . Since the integral closure of $(\overline {I^n})^{p}$ coincides with $\overline {I^{n p}}$ for p large, we have

$$ \begin{align*} \bar{e}_0(I^{n})= n^2 \bar{e}_0(I); \ \ \bar{e}_1(I^{n}) = n \bar{e}_1(I) + {n \choose 2} \bar{e}_0(I); \ \ \bar{e}_2(I^n)= \bar{e}_2(I). \end{align*} $$

After substituting the $\bar {e}_i(I^n)$ ’s with the corresponding expressions in terms of the $\bar {e}_i(I)$ ’s we conclude that

$$ \begin{align*} \bar{e}_2(I^n) - \bar{e}_1(I^n) + \bar{e}_0(I^n)-\ell_A(A/\overline{I^n}) &= \bar{e}_0(I) {n+1 \choose 2} - \bar{e}_1(I) n + \bar{e}_2(I) -\ell_A(A/\overline{I^n}) \\ &= \bar{P}_I(n-1) -\ell_A(A/\overline{I^n}) =0. \end{align*} $$

Since I is not a $p_g$ -ideal, then $\bar {e}_2(I^n)= \bar {e}_2(I)>0. $ Hence, by Theorem 3.2, then $\overline {I^n}$ is an elliptic ideal.

We denote by $\mathfrak {M} = \mathfrak m + \bar {\mathcal R}_{+} $ the homogeneous maximal ideal of $\bar {\mathcal R}$ . As usual, we say that $\bar {\mathcal R}$ is $($ FLC $)$ if $\ell _A(H^i_{\mathfrak {M}} (\bar {\mathcal R}))< \infty $ for every $i \le \dim A=2$ .

Proposition 3.4. Assume I is an elliptic ideal, then $\bar {\mathcal R}$ is $($ FLC $)$ but not Cohen–Macaulay with

$$ \begin{align*} H^2_{\mathfrak M}(\bar{\mathcal R}) = [H^2_{\mathfrak M}(\bar{\mathcal R})]_0 \cong [H_{\mathfrak M}^2(\bar{G})]_0. \end{align*} $$

Proof. Note that $\bar {\mathcal R}_{\mathfrak M}$ is a universally catenary domain which is a homomorphic image of a Cohen–Macaulay local ring. Hence, it is an (FLC) because $\bar {\mathcal R}$ satisfies Serre condition $(S_2)$ . Thus, $H_{\mathfrak M}^0(\bar {\mathcal R})= H_{\mathfrak M}^1(\bar {\mathcal R})=0$ and $H_{\mathfrak M}^2(\bar {\mathcal R})$ has finite length.

Put $\mathcal {N}=\bar {\mathcal R}_{+}$ . Then we obtain two exact sequences of graded $\bar {\mathcal R}$ -modules.

$$ \begin{align*} 0 \to \mathcal{N} \to \bar{\mathcal R} \to {}_h A \to 0, \; \end{align*} $$

$$ \begin{align*} 0 \to \mathcal{N}(1) \to \bar{\mathcal R} \to \bar{G} \to 0, \; \end{align*} $$

where ${}_h A$ can be regarded as $\bar {\mathcal R}/\mathcal {N}$ which is concentrated in degree $0$ . One can easily see that $H_{\mathfrak M}^0(\mathcal {N})=H_{\mathfrak M}^1(\mathcal {N})=0$ , and we get

(3.1) $$ \begin{align} 0 \to H_{\mathfrak M}^2(\mathcal{N}) \to H_{\mathfrak M}^2(\bar{\mathcal R}) \to {}_h H_{\mathfrak m}^2(A) \to H_{\mathfrak M}^3(\mathcal{N}) \to H_{\mathfrak M}^3(\bar{\mathcal R}) \to 0, \; \end{align} $$

(3.2) $$ \begin{align} 0 \to H_{\mathfrak M}^2(\mathcal{N})(1) \to H_{\mathfrak M}^2(\bar{\mathcal R}) \to H_{\mathfrak M}^2(\overline{G}) \to H_{\mathfrak M}^3(\mathcal{N})(1) \to H_{\mathfrak M}^3(\bar{\mathcal R}) \to 0. \; \end{align} $$

For any integer $n \le -1$ , the first exact sequence (3.1) yields

$$ \begin{align*} 0\to [H_{\mathfrak M}^2(\mathcal{N})]_n \to [H_{\mathfrak M}^2(\bar{\mathcal R})]_n \to 0. \; \end{align*} $$

In addition, the second exact sequence (3.2) yields

$$ \begin{align*} 0=[H_{\mathfrak M}^1(\bar{G})]_n \to [H_{\mathfrak M}^2(\mathcal{N})]_{n+1} \to [H_{\mathfrak M}^2(\bar{\mathcal R})]_n. \; \end{align*} $$

Then $[H_{\mathfrak M}^2(\bar {\mathcal R})]_{-1} \subset [H_{\mathfrak M}^2(\bar {\mathcal R})]_{-2} \subset \cdots \subset [H_{\mathfrak M}^2(\bar {\mathcal R})]_{n}=0$ for $n \ll 0$ , and thus $[H_{\mathfrak M}^2(\bar {\mathcal R})]_{n}=0$ for all $n \le -1$ .

For any integer $n \ge 1$ , the first exact sequence (3.1) yields

$$ \begin{align*} 0 \to [H_{\mathfrak M}^2(\mathcal{N})]_n \to [H_{\mathfrak M}^2(\bar{\mathcal R})]_n \to 0. \; \end{align*} $$

Moreover, as $a(\bar {G})=0$ , we have

$$ \begin{align*} [H_{\mathfrak M}^2(\mathcal{N})]_{n+1} \to [H_{\mathfrak M}^2(\bar{\mathcal R})]_n \to [H_{\mathfrak M}^2(\bar{G})]_n =0 \; \text{(ex)}. \end{align*} $$

Hence, we get $[H_{\mathcal {M}}^2(\bar {\mathcal R})]_n=0$ for all $n \ge 1$ .

Since $a(\bar {\mathcal R})=-1$ , we have $[H_{\mathfrak M}^3(\mathcal {N})]_1 \cong [H_{\mathfrak M}^3(\bar {\mathcal R})]_1=0$ . Hence, we get

$$ \begin{align*} H_{\mathfrak M}^2(\bar{\mathcal R})= [H_{\mathfrak M}^2(\bar{\mathcal R})]_0 \cong [H_{\mathfrak M}^2(\bar{G})]_0, \end{align*} $$

as required.

Corollary 3.5. Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain, and let $I \subset A$ be an $\mathfrak m$ -primary integrally closed ideal.

Then I is an elliptic ideal if and only if $0 \ne H^2_{\mathfrak M}(\bar {\mathcal R}) = [H^2_{\mathfrak M}(\bar {\mathcal R})]_0 \hookrightarrow H_{\mathfrak m}^2(A)$ , where the last map is induced from the natural surjection $\bar {\mathcal R} \to {}_h A = \bar {\mathcal R}/\bar {\mathcal R}_{+}$ .

Proof. Assume I is an elliptic ideal, then from the proof of Proposition 3.4 and Theorem 3.2, we conclude our assertions. Conversely, by our assumption, we can conclude that $\bar {G}(I)$ is Cohen–Macaulay with $a(\bar {G}(I))=0$ by a similar argument as in the proof of Proposition 3.4. Hence, I is an elliptic ideal by Theorem 3.2.

For a cycle $C>0$ on X, we denote by $\chi (C)$ the Euler characteristic of $\mathcal O_C$ .

Definition 3.6. Let $Z_f$ denote the fundamental cycle, namely, the nonzero minimal anti-nef cycle on X. The ring A is called elliptic if $\chi (Z_f)=0$ .

The following result follows from Theorem 3.2 and [22, Theorem 3.3].

Corollary 3.7. If A is an elliptic singularity, then for every integrally closed ideal $I \subset A$ , the following facts hold $:$

1. (1) $\bar {G}(I)$ is Cohen–Macaulay with $a(\bar {G}(I))\le 0$ .

2. (2) I is elliptic or a $p_g$ -ideal.

Since there always exists an ideal I with $q(I)=0$ , we have $\bar r(A)=2$ .

The result above gives some evidence about a positive answer to the following question:

Question 3.8. Assume $\bar r(A) =2$ , is it true that A is an elliptic singularity?

We can give a positive answer to Question 3.8 if $ \bar {e}_2(I) \le 1$ for all integrally closed $\mathfrak m$ -primary ideals. In the following result, we describe the integrally closed $\mathfrak m$ -primary ideals satisfying this minimal condition.

Theorem 3.9. Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain over an algebraically closed field. Let $I \subset A$ be an $\mathfrak m$ -primary integrally closed ideal, and let Q be a minimal reduction of I. Put $\bar {G}=\bar {G}(I)$ and $\bar {\mathcal R}=\bar {\mathcal R}(I)$ . Then the following conditions are equivalent $:$

1. (1) $\bar {r}(I)=2$ and $\ell _A(\overline {I^2}/Q I) =1$ .

2. (2) $q(I)=q(\infty I)=p_g(A)-1$ .

3. (3) $\bar {e}_2(I) =1$ .

4. (4) $\bar {e}_1(I) = e_0(I) -\ell _A( A/I) + 1$ and $\operatorname {\mathrm {nr}}(I)=\bar {\mathrm {r}}(I)$ .

5. (5) $\bar {G}$ is Cohen–Macaulay with $a(\bar {G})=0$ and $\ell _A([H^2_{\mathfrak M}(\bar {G})]_0)=1$ .

When this is the case, I is said to be a strongly elliptic ideal and $\bar {\mathcal R}$ is a Buchsbaum ring with $\ell _A(H^2_{\mathfrak M}(\bar {\mathcal R})) = 1$ .

Proof. $(1) \Longrightarrow (2):$ By Theorem 3.2, we have $p_g(A)> q(I)=q(\infty I)$ . In particular, $q(2 I)=q(I)$ . By Proposition 2.5(1), $p_g(A)-q(I)=\ell _A(\overline {I^2}/QI)=1$ . Conversely, $(2) \Longrightarrow (1) $ again by Proposition 2.5.

$(2) \Longrightarrow (3):$ By Proposition 2.6(4), we have

$$ \begin{align*} \bar{e}_2(I)=p_g(A)-q(I)=1. \end{align*} $$

$(3) \Longrightarrow (2):$ Since $p_g(A)-q(\infty I)=\bar {e}_2(I)=1$ , by assumption, we have $p_g(A)-1 = q(\infty I) \le q(I) \le p_g(A)$ . If $q(I)=p_g(A)$ , then I is a $p_g$ -ideal, and thus $\bar {e}_2(I)=0$ . This is a contradiction. Hence, $q(\infty I) = q(I)=p_g(A)-1$ , as required.

$(1),(3) \Longrightarrow (4):$ It follows from Theorem 3.2 $(1)\Longrightarrow (3)$ and the fact that $1< \operatorname {\mathrm {nr}}(I) \le \bar {\mathrm {r}}(I)=2. $

$(4) \Longrightarrow (1):$ By Proposition 2.5(1), we have

$$ \begin{align*} \ell_A(\overline{I^2}/QI)&= (p_g(A)-q(I))-(q(I)-q(2I)), \\ \ell_A(\overline{I^3}/Q\overline{I^2})&= (q(I)-q(2I))-(q(2I)-q(3I)), \\ \vdots \qquad ~ &= ~ \qquad \vdots \end{align*} $$

By a similar argument as in [10] and Proposition 2.6, we get

$$ \begin{align*} \bar{e}_2(I) &= \sum_{n=1}^{\infty} n \cdot \ell_A(\overline{I^{n+1}}/Q\overline{I^n}), \\ \bar{e}_1(I)-\bar{e}_0(I)+\ell_A(A/I) &= \sum_{n=1}^{\infty} \ell_A(\overline{I^{n+1}}/Q\overline{I^n}). \end{align*} $$

Thus, our assumption implies $\ell _A(\overline {I^{n+1}}/Q\overline {I^n})=1$ for some unique integer $n \ge 1$ . On the other hand, since $\operatorname {\mathrm {nr}}(I)=\bar {\mathrm {r}}(I)$ , we must have $n=1$ .

$(1) \Longrightarrow (5):$ Suppose (1). Then Theorem 3.2 $(1)\Longrightarrow (5)$ implies that $\bar {G}$ is Cohen–Macaulay with $a(\bar {G})=0$ .

We remark that $\sqrt {\mathfrak M} = \sqrt {\bar G_+} $ in $\bar G; $ hence, by [19, Proposition 3.1], we have $[H_{\mathfrak M}^2(\bar G)]_0 \cong \overline {I^2}/QI \cong A/\mathfrak m$ has length $1$ . In particular, by Proposition 3.4, $H_{\mathfrak M}^2(\bar {\mathcal R})$ becomes an $A/\mathfrak m$ -vector space, and thus $\bar {\mathcal R}$ is Buchsbaum.

$(5) \Longrightarrow (1):$ By Theorem 3.2 $(5) \Longrightarrow (1)$ , we have $\bar {\mathrm {r}}(I)=2$ . In addition, $\ell _A(\overline {I^2}/QI)=\ell _A([H_{\mathfrak M}^2(\bar {G})]_0)=1$ .

It is clear that if I is a strongly elliptic ideal, then I is an elliptic ideal. In some cases, they are equivalent. Notice that the converse is not true in general. For instance, let $A=k[[x^2,y^2,z^2,xy,xz,yz]]/(x^4+y^4+z^4)$ . Then A is a two-dimensional normal local domain with the maximal ideal $\mathfrak m=(x^2,y^2,z^2,xy,xz,yz)$ . Then $\mathfrak m$ is a normal ideal, and $Q=(x^2,y^2)$ is a minimal reduction of $\mathfrak m$ with $\mathfrak m^3=Q\mathfrak m^2$ . Moreover, $\bar {\mathrm {r}}(\mathfrak m)=r(\mathfrak m)=2$ and $\ell _A(\mathfrak m^2/Q\mathfrak m)=3$ imply that $\mathfrak m$ is an elliptic ideal but not a strongly elliptic ideal.

Notice that (1) is equivalent to (3) follows also from [13].

Proposition 3.10. Let $(A,\mathfrak m)$ be a two-dimensional Gorenstein excellent normal local domain. Then $\mathfrak m$ is an elliptic ideal if and only if $\mathfrak m$ is a strongly elliptic ideal.

Proof. Assume $\mathfrak m$ is an elliptic ideal and Q be its minimal reduction. Since $\bar {r}(\mathfrak m)=2$ , $\mathfrak m \overline {\mathfrak m^2} \subset Q$ , and we have $\overline {\mathfrak m^2}/Q\mathfrak m \cong (\overline {\mathfrak m^2}+Q)/Q \hookrightarrow A/Q$ , whose image is contained in $(Q:\mathfrak m)/Q$ . Since the latter has length $1$ , $\ell _A (\overline {\mathfrak m^2}/Q\mathfrak m) =1$ and $\mathfrak m$ is strongly elliptic.

Example 3.11. Let $A=\mathbb {C}[[x,y,z]]/(x^a+y^b+z^c)$ be a Brieskorn hypersurface, where $2 \le a \le b \le c$ . Then:

1. (1) $\mathfrak m$ is a $p_g$ -ideal if and only if $(a,b)=(2,2),(2,3)$ .

2. (2) $\mathfrak m$ is an elliptic ideal (equivalently strongly elliptic) if and only if

   $$ \begin{align*} (a,b)=(2,4),(2,5),(3,3),(3,4). \end{align*} $$

In particular, if $p \ge 1$ and $(a,b,c)=(2,4,4p+1)$ , then $p_g(A)=p$ and $\mathfrak m$ is a (strongly) elliptic ideal. It follows from [26, Theorem 3.1 and Proposition 3.8].

Example 3.12. Proposition 3.10 does not hold if $I \neq \mathfrak m$ . Let A be any two-dimensional excellent normal local domain with $p_g(A)> 1$ . Then there exist always integrally closed ideals I with $q(I)=0$ . Since $q(I)=q(2I)=0$ , $\bar {r}(I) =2$ , and $\bar {e}_2(I) = p_g(A)$ . Thus, 3.10 does not hold for such I.

We recall that an excellent normal local domain for which every integrally closed $\mathfrak m$ -primary ideal is a $p_g$ -ideal is a rational singularity ( $p_g(A)=0$ ). This result suggests to study the next step.

Definition 3.13 (e.g., [41])

An excellent normal local domain A is a strongly elliptic singularity if $p_g(A)=1$ .

Note that any strong elliptic singularity is an elliptic singularity. The following result characterizes algebraically the strongly elliptic singularities.

Theorem 3.14. Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain containing an algebraically closed field $k= A/\mathfrak m$ and assume that $p_g(A)>0$ . The following facts are equivalent $:$

1. (1) A is a strongly elliptic singularity.

2. (2) Every integrally closed ideal of A is either a $p_g$ -ideal or a strongly elliptic ideal.

Proof. It depends by the fact that always there exists an integrally closed ideal I of A such that $q(I)=0$ . Thus, $p_g(A)= \bar {e}_2(I)$ .

If A is a rational singularity, then every integrally closed $\mathfrak m$ -primary ideal is normal. This is not true if A is an elliptic singularity, even if we assume A is a strongly elliptic singularity.

Example 3.15.

1. (1) Let $A = k[ X,Y,Z]/ (X^3 + Y^3 + Z^3), $ then A is Gorenstein, $p_g(A) = 1$ , and the maximal ideal $\mathfrak m$ is normal. If we consider $I = (x,y, z^2), $ then $I^2$ is not normal.

2. (2) Cutkosky showed that if $A= \mathbb {Q}[[ X,Y,Z]]/ (X^3 +3 Y^3 +9 Z^3)$ ( $\mathbb {Q}$ rational numbers), then for every integrally closed ideal $I \subset A$ , $I^2 $ is also integrally closed and hence normal. This is because the elliptic curve does not have any $\mathbb {Q}$ -rational point.

3. (3) Let $A=k[x,y,z]/(x^2+y^4+z^4)$ , $I=\mathfrak m=(x,y,z)$ , and $Q=(y,z)$ . Then $p_g(A)=1$ and $ \overline {\mathfrak m^n}= x(y,z)^{n-2}+\mathfrak m^n$ for every $n \ge 2$ .

Proposition 3.16. Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain containing an algebraically closed field $k= A/\mathfrak m. $ Assume that I is a strongly elliptic ideal. Then the following conditions are equivalent $:$

1. (1) $\overline {I^2}=I^2$ .

2. (2) $\overline {I^n}=I^n$ for some $n \ge 2$ .

3. (3) $\overline {I^n}=I^n$ for every $n \ge 2$ .

Proof. By Theorem 3.9(1), we have $\ell _A(\overline {I^2}/QI)=1$ and $\overline {I^n} = Q \overline {I^{n-1}}$ for $n\ge 3$ . Hence, if $I^2 = \overline {I^2}$ , then $I^n = \overline {I^n}$ for all $n\ge 2$ .

Conversely, assume that $I^2 \ne \overline {I^2}$ . Since $\ell _A(\overline {I^2}/QI)=1$ , we should have $I^2 = QI$ . This implies that $G(I) := \oplus _{n\ge 0} I^n/ I^{n+1}$ is Cohen–Macaulay with $a(G(I)) = -1$ (see [8], [37, Proposition 2.6]) and hence

$$ \begin{align*} \ell_A( A/ I^{n+1}) = e_0(I) \genfrac{(}{)}{0pt}{0}{n+2}{2} - e_1(I)\genfrac{(}{)}{0pt}{0}{n+1}{1} \end{align*} $$

with $e_0(I) = \bar e_0(I)$ and $e_1(I) = e_0(I) - \ell _A(A/I)$ .

On the other hand, by Theorem 3.2 and Corollary 3.9, we have

$$ \begin{align*} \ell_A(A/\overline{I^{n+1}})&= \bar{P}_I(n)=\overline{e}_0(I){n+2 \choose 2} - \overline{e}_1(I){n+1 \choose 1} + \overline{e}_2(I) \\ &= e_0(I){n+2 \choose 2} - (e_0(I)-\ell_A(A/I)+1){n+1 \choose 1} +1 \\ &= \ell_A(A/I^{n+1})-n. \end{align*} $$

This implies that $I^n \ne \overline {I^n}$ for all $n\ge 2$ .

We can characterize the normal ideals in a strongly elliptic singularity. Before showing the results, let us recall some definitions and basic facts on cycles and a vanishing theorem for elliptic singularities. In the following, A is an elliptic singularity, and X is a resolution of $\operatorname {\mathrm {Spec}}(A)$ .

For a cycle $C>0$ on X, we denote by $\chi (C)$ the Euler characteristic $\chi (\mathcal O_C)=h^0(\mathcal O_C)-h^1(\mathcal O_C)$ . Then $p_a(C):=1-\chi (C)$ is called the arithmetic genus of C. By the Riemann–Roch theorem, we have $\chi (C)=-(K_X+C)C/2$ , where $K_X$ is the canonical divisor on X. From this, if $C_1, C_2>0$ are cycles, we have $\chi (C_1+C_2)=\chi (C_1)+\chi (C_2)-C_1C_2$ . From the exact sequence

$$ \begin{align*} 0\to \mathcal O_{C_2}(-C_1) \to \mathcal O_{C_1+C_2} \to \mathcal O_{C_1} \to 0, \end{align*} $$

we have $\chi (\mathcal O_{C_2}(-C_1))=-C_1C_2+\chi (C_2)$ .

If A is elliptic, then there exists a unique cycle $E_{min}$ , called the minimally elliptic cycle, such that $\chi (E_{min})=0$ and $\chi (C)>0$ for all cycles $0<C<E_{min}$ (see [15]). Moreover, we have the following (see [15, Propositions 3.1 and 3.2 and Corollary 4.2], [36, (6.4) and (6.5)], [38, p. 428]).

Proposition 3.17. Assume that A is elliptic. Then $\chi (C)\ge 0$ for any cycle $C>0$ on X and $C\ge E_{min}$ if $\chi (C)=0$ .

Let us recall that the fundamental cycle $Z_f$ can be computed via a sequence of cycles:

$$ \begin{align*} C_0:=0, \quad C_1=E_{j_1}, \quad C_i=C_{i-1}+E_{j_i}, \quad C_m=Z_f, \end{align*} $$

where $E_{j_1}$ is an arbitrary component of E and $C_{i-1}E_{j_i}>0$ for $2\le i \le m$ . Such a sequence $\{C_i\}$ is called a computation sequence for $Z_f$ . It is known that $h^0(\mathcal O_{C_i})=1$ for $1 \le i\le m$ (see [15, p. 1,260]).

The following vanishing theorems are essential in our argument.

Theorem 3.18 (Röhr [31, 1.7])

Let L be a divisor on X such that $LC>-2\chi (C)$ for every cycle $C>0$ which occurs in a computation sequence for $Z_f$ . Then $H^1(\mathcal O_X(L))=0$ . If A is rational, then the converse holds, too.

From Theorem 3.18 and Proposition 3.17, we have the following.

Corollary 3.19. Assume that A is an elliptic singularity. Let L be a nef divisor on X such that $L E_{min}>0$ . Then $H^1(\mathcal O_X(L))=0$ .

Proposition 3.20. Assume that A is an elliptic singularity and D the minimally elliptic cycle on X. Let F be a nef divisor on X. If $FD>0$ , then $H^1(\mathcal O_X(F-D))=0$ , and from the exact sequence $0 \to \mathcal O_X(F-D) \to \mathcal O_X(F) \to \mathcal O_D(F) \to 0$ , the restriction map $H^0(\mathcal O_X(F))\to H^0(\mathcal O_D(F))$ is surjective.

Proof. If $F-D$ is nef, since $(F-D)D>0$ , we have $H^1(\mathcal O_X(F-D))=0$ by Corollary 3.19. Assume that $F-D$ is not nef. As in [6, 1.4], we have a sequence $\{D_i\}$ of cycles such that

$$ \begin{align*} D_0=D, \ \ D_i = D_{i-1} + E_{j_i}, \; (F-D_{i-1}) E_{j_i}<0\; (1\le i \le s), \ \ F-D_{s} \text{ is nef.} \end{align*} $$

Since $F-Z_f$ is nef, $(F-D_{i-1}) E_{j_i}<0$ implies $D_{i-1}E_{j_i}>0$ , and $D\le Z_f$ , we see that $D_s\le Z_f$ and $D_s$ occurs in a computation sequence for $Z_f$ . Then the equalities $\chi (D)=\chi (D_s)=0$ and $\chi (D_i) = \chi (D_{i-1}) +\chi ( E_{j_i})-D_{i-1} E_{j_i}$ imply that $F E_{j_i}=0$ , $D_{i-1} E_{j_i}=1$ , and $h^j(\mathcal O_{E_{j_i}}(F-D_{i-1}))=0$ for $j=0,1$ and $1\le i \le s$ . Since

$$ \begin{align*} 0\le \chi(D_s+D)=\chi(D_s)+\chi(D)-DD_s=-DD_s, \end{align*} $$

we have $(F-D_s)D>0$ . Therefore, from the exact sequence

$$ \begin{align*} 0 \to \mathcal O_X(F-D_i) \to \mathcal O_X(F-D_{i-1}) \to \mathcal O_{E_{j_i}}(F-D_{i-1}) \to 0, \end{align*} $$

we obtain $H^1(\mathcal O_X(F-D))=H^1(\mathcal O_X(F-D_s))=0$ .

Theorem 3.21 [5, 2.7]

Let C be a Cohen–Macaulay projective scheme of pure dimension $1$ , and let $\mathcal F$ be a rank $1$ torsion-free sheaf on C. Assume that $\deg \mathcal F|_{W}:= \chi (\mathcal F|_{W})-\chi (W)> -2\chi (W)$ for every subcurve $W\subset C$ . Then $H^1(\mathcal F)=0$ .

To show the normality of an ideal I, the following is essential.

Proposition 3.22. Let $\mathcal L_1$ and $\mathcal L_2$ be nef invertible sheaves on the minimally elliptic cycle D such that $d_i:=\deg \mathcal L_i \ge 3$ for $i=1,2$ . Then the multiplication map

$$ \begin{align*} \gamma: H^0(\mathcal L_1)\otimes H^0(\mathcal L_2) \to H^0(\mathcal L_1\otimes \mathcal L_2) \end{align*} $$

is surjective.

Proof. First, note that $\chi (W)>0$ for any cycle $0<W\lneqq D$ by the definition of the minimally elliptic cycle. For any subscheme $\Lambda \subset D$ , we denote by $I_{\Lambda }\subset \mathcal O_D$ the ideal sheaf of $\Lambda $ . For any cycle $W\le D$ and any $p\in \operatorname {\mathrm {Supp}} (W)$ , we have $\deg (I_p\mathcal L_i)|_W=\deg \mathcal L_i|_W-1$ . Therefore, it follows from Theorem 3.21 that $H^1(I_p\mathcal L_i)=0$ for any point $p \in \operatorname {\mathrm {Supp}}(D)$ . Hence, $\mathcal L_i$ is generated by global sections. Let $s\in H^0(\mathcal L_1)$ be a general section and consider the exact sequence

(3.3) $$ \begin{align} 0\to \mathcal O_D \xrightarrow{ \times s } \mathcal L_1 \to \mathcal L_1|_B \to 0, \end{align} $$

where B is the zero-dimensional subscheme of D of degree $d_1=\deg \mathcal L_1$ defined by s. Note that since $\mathcal L_1$ is generated by global sections, each point of $\operatorname {\mathrm {Supp}} (B)$ is a nonsingular point of $\operatorname {\mathrm {Supp}} (D)$ and there exists $s_1\in H^0(\mathcal L_1)$ such that $\mathcal L_1|_B\cong s_1\mathcal O_B\cong \mathcal O_B$ . Let $p\in \operatorname {\mathrm {Supp}}(B)$ be any point. The following fact makes our proof easier.

Claim 7. Let $\mathfrak n \subset \mathcal O:=\mathcal O_{X,p}$ be the maximal ideal. Then we can take generators $x,y$ of $\mathfrak n$ , so that $\mathcal O_{D,p}=\mathcal O/(x^{n_p})$ with $n_p\ge 1$ and $\mathcal O_{B,p}\cong \mathcal O/(x^{n_p},y)$ . Hence, at p, the subschemes of B correspond to monomials $x^{\ell }$ with $\ell \le n_p$ .

Proof of Claim 7

Since E is nonsingular at p, we have the generators $x,y\in \mathfrak n$ such that $\mathcal O_{D,p}=\mathcal O/(x^{n_p})$ . Assume that $\mathcal O_{B,p}=\mathcal O/(x^{n_p}, f)$ , where $f\in \mathfrak n$ . If $\ell _{\mathcal O}(\mathcal O/(x,f))=1$ , we can put $y=f$ . Assume that $\ell _{\mathcal O}(\mathcal O/(x,f))\ge 2$ . Let $0<W\le D$ be any cycle, and let $\mathcal O_{W,p}=\mathcal O/(x^{m_p})$ . Assume that $p\in \operatorname {\mathrm {Supp}} (W)$ . Then the cokernel of $(I_p^2\mathcal L_1)|_W\to \mathcal L_1|_W$ is isomorphic to $\mathcal O/\mathfrak n^2+(x^{m_p})$ . If $m_p=1$ , then $\deg (I_p^2\mathcal L_1)|_W=\deg \mathcal L_1|_W-2$ . If $m_p\ge 2$ , then $\deg (I_p^2\mathcal L_1)|_W =\deg \mathcal L_1|_W-3\ge \ell _{\mathcal O}(\mathcal O/(x^{m_p},f))-3\ge 1$ . Thus, we have $H^1(I_p^2\mathcal L_1)=0$ by Theorem 3.21, and the map $H^0(I_p\mathcal L_1) \to I_p\mathcal L_1/I_p^2\mathcal L_1$ is surjective; however, this shows that we can take $f=y$ .

Tensoring $\mathcal L_2$ with the sequence (3.3), we obtain the exact sequence

$$ \begin{align*} 0\to H^0( \mathcal L_2) \xrightarrow{ \times s } H^0(\mathcal L_1 \otimes \mathcal L_2) \to H^0(\mathcal O_B) \to 0, \end{align*} $$

since $H^1(\mathcal L_2)=0$ . As seen above, we have general sections $s_1\in H^0(\mathcal L_1)$ and $s_2\in H^0(\mathcal L_2)$ such that $s_1s_2\mapsto 1\in H^0(\mathcal O_B)$ . Thus, the sections of $H^0(\mathcal L_1 \otimes \mathcal L_2)$ which map to $1\in H^0(\mathcal O_B)$ are in the image of $\gamma $ . It is now sufficient to show that for any subscheme $B'\subset B$ of $\deg B'<d_1$ , the image of $\gamma $ contains a section $t \in H^0(\mathcal I_{B'}\mathcal L_1\otimes \mathcal L_2)$ such that $\mathcal L_1\otimes \mathcal L_2/t\mathcal O_D \cong \mathcal O_{B'}\oplus \mathcal O_{\overline {B}}$ , where $\operatorname {\mathrm {Supp}} (\overline {B}) \cap \operatorname {\mathrm {Supp}} (B)=\emptyset $ . To prove this, we write $\mathcal I_{B'}=\mathcal I_{B_1}\mathcal I_{B_2}$ ( $B_1, B_2\subset B'$ ), so that $\deg \mathcal I_{B_i}\mathcal L_i=d_i-\deg B_i\ge 2$ for $i=1,2$ (note that $\deg B_1 + \deg B_2 <d_1$ ). Let $0<W\le D$ be any cycle, and let $p\in \operatorname {\mathrm {Supp}}(B)$ . We use the notation of the proof of Claim 7. Suppose that $\mathcal O_{B_1,p}=\mathcal O/(x^{\ell _p},y)$ . Then $\deg \mathcal L_1|_W=\sum _W m_p$ , where $\sum _W$ means the sum over $p\in \operatorname {\mathrm {Supp}}(B) \cap \operatorname {\mathrm {Supp}}(W)$ , and the cokernel of $(I_{B_1}\mathcal L_1)|_W\to \mathcal L_1|_W$ is isomorphic to $\mathcal O/(x^{m_p}, x^{\ell _p},y)$ . Therefore,

$$ \begin{align*} \deg(I_{B_1}\mathcal L_1)|_W=\sum_W (m_p-\min(m_p, \ell_p)). \end{align*} $$

Since $\deg \mathcal I_{B_1}\mathcal L_1=d_1-\deg B_1\ge 2$ , by Theorem 3.21, we have $H^1(I_q\mathcal I_{B_1}\mathcal L_1)=0$ for any point $q\in \operatorname {\mathrm {Supp}}(B)$ . Hence, $H^0(\mathcal I_{B_1}\mathcal L_1)$ has no base points. Clearly, the same results for $\mathcal I_{B_2}\mathcal L_2$ hold. Therefore, for each $i=1,2$ , we have a section $t_i\in H^0(\mathcal I_{B_i}\mathcal L_i)$ such that $\mathcal L_i/t_i\mathcal O_D \cong \mathcal O_{B_i}\oplus \mathcal O_{\overline {B_i}}$ , where $\operatorname {\mathrm {Supp}} (\overline {B_i}) \cap \operatorname {\mathrm {Supp}} (B)=\emptyset $ . Then $t:=t_1t_2$ satisfies the required property.

Theorem 3.23. Let $(A,\mathfrak m)$ be a two-dimensional excellent normal local domain containing an algebraically closed field $k= A/\mathfrak m$ . Assume that A is a strongly elliptic singularity. If $I = I_Z $ is an elliptic ideal $($ equivalently, I is not a $p_g$ -ideal $)$ and D is the minimally elliptic cycle on X, then $I^2$ is integrally closed $($ equivalently, I is normal $)$ if and only if $- Z D \ge 3$ and if $- ZD \le 2$ , then $I^2 = QI$ .

Proof. Assume that $-ZD\le 2$ . Since $H^1(\mathcal O_X(-Z))=0$ , by the Riemann–Roch theorem, we have $h^0(\mathcal O_D(-nZ))=-nZD$ for $n\ge 1$ . Hence,

$$ \begin{align*} H^0(\mathcal O_D(-Z))\otimes H^0(\mathcal O_D(-Z)) \to H^0(\mathcal O_D(-2Z)) \end{align*} $$

cannot be surjective. By Proposition 3.20, the map

$$ \begin{align*} H^0(\mathcal O_X(-Z))\otimes H^0(\mathcal O_X(-Z)) \to H^0(\mathcal O_X(-2Z)) \end{align*} $$

cannot be surjective, too. Therefore, $I^2\ne I_{2Z}$ , and hence $I^2 = QI$ .

Assume that $-ZD\ge 3$ . By Propositions 3.20 and 3.22, we have the following commutative diagram:

where at least the maps other than $\alpha $ are surjective. By Proposition 3.20 and its proof, we have $I_{2Z}=I^2+H^0(\mathcal O_X(-2Z-D))$ , $H^0(\mathcal O_X(-2Z-D))=H^0(\mathcal O_X(-2Z-D_s))$ , and $-(Z+D_s)D\ge -ZD\ge 3$ . We have as above a surjective map

$$ \begin{align*} H^0(\mathcal O_D(-Z))\otimes H^0(\mathcal O_D(-Z-D_s)) \to H^0(\mathcal O_D(-2Z-D_s)) \end{align*} $$

and $H^0(\mathcal O_X(-2Z-D_s)) \subset I H^0(\mathcal O_X(-Z-D_s))+H^0(\mathcal O_X(-2Z-D_s-D))$ . From these arguments, for $m>0$ , we have $I_{2Z}\subset I^2+H^0(\mathcal O_X(-2Z-mD))$ . We denote by $H(m)$ the minimal anti-nef cycle on X such that $H(m)\ge 2Z+mD$ . Then $H^0(\mathcal O_X(-2Z-mD))=H^0(\mathcal O_X(-H(m)))$ , and for an arbitrary $n\in \mathbb Z_{+}$ , there exists $m(n)\in \mathbb Z_{+}$ such that $H(m(n))\ge nE$ . Therefore, $H^0(\mathcal O_X(-2Z-mD))\subset I^2$ for sufficiently large m, and we obtain $I_{2Z}=I^2$ .

Remark 3.24. Assume that A is elliptic. It follows from Proposition 4.5 and Corollary 3.19 that $q(I)=0$ if and only if $ZD\ne 0$ . By an argument similar to the proof of Theorem 3.23, we can prove that if $ZD\ne 0$ , then $I=I_Z$ is normal if and only if $-ZD\ge 3$ .

For elliptic ideals in an elliptic singularity (not strongly elliptic), Remark 3.24 cannot be applied because the condition $ZD \ne 0$ does not hold in general. Next example shows that the condition $0 < -ZD <3$ is not necessary for $I_Z$ being not normal.

Example 3.25. Suppose that $p\ge 1$ be an integer. Let $ A=k[x,y,z]/(x^2+y^3+z^{6(p+1)})$ , and assume that X is the minimal resolution. Then E is a chain of $p+1$ nonsingular curves $E_0, E_1, \dots , E_p$ , where $g(E_0)=1$ , $E_0^2=-1$ , $g(E_i)=0$ , $E_i^2=-2$ , $E_{i-1}E_i=1$ , for $1\le i \le p$ , and $E_iE_j =0$ if $|i-j| \ge 2$ . It is easy to see that A is elliptic and $E_0$ is the minimally elliptic cycle. Furthermore, $\mathfrak m$ is a $p_g$ -ideal and $p_g(A)=p+1$ by [26, 3.1 and 3.10]. Since A is not strongly elliptic, there is a non- $p_g$ -ideal $I_Z$ such that $-ZE_0=0$ (see Theorem 3.14 and Proposition 4.5). Let $W=\sum _{i=0}^p(p+1-i)E_i$ . Then $-W\sim K_X$ and the exceptional part of the divisors $\operatorname {\mathrm {div}}_X(x)$ , $\operatorname {\mathrm {div}}_X(y)$ , and $\operatorname {\mathrm {div}}_X(z)$ are $3W$ , $2W$ , and E, respectively. For $1\le n \le p+1$ , let $D_n=\gcd (nE, W):=\sum _{i=0}^p\min (n,p+1-i)E_i$ . (Our cycle $D_n$ coincides with $C_{n-1}$ in [22, 2.6].) Then $\mathcal O_X(-2D_n)$ is generated (cf. [22, 3.6(4)]) and $D_n^2=-n$ . Let $I_n=I_{2D_n}$ . Since the cohomological cycle of $(D_n)^{\bot }$ is $W-D_n$ , we have $q(I_n)=p_g(A)-n$ by Proposition 4.5; note that $-(W-D_n)\sim K_X$ on a neighborhood of $\operatorname {\mathrm {Supp}}(W-D_n)=E_0\cup \cdots \cup E_{p-n}$ . Then $I_n=(x,y,z^{2n})$ . We have $D_nE_0=0$ for $1\le n\le p$ and $D_{p+1}E_0=E_0^2=-1$ . Therefore, it follows from Remark 3.24 that $\overline {I_{p+1}^2}\ne I_{p+1}^2$ , since $-2D_{p+1}E_0=2$ . However, the condition $0<-ZE_0\le 2$ is not necessary for $I_Z$ being not normal. In fact, we have $\overline {I_{n}^2}\ne I_{n}^2$ for all $1\le n \le p+1$ because $xz^n\not \in I_n^2$ and $(xz^n)^2\in I_n^4$ .

4 The existence of strongly elliptic ideals

Motivated by the fact that in every two-dimensional excellent normal local domain which is not a rational singularity elliptic ideals always exist, it is natural to ask if it is also true for strongly elliptic ideals. We need some more preliminaries for proving that the answer is negative, in particular there are two-dimensional excellent normal local domains with no integrally closed $\mathfrak m$ -primary ideals I with $\bar e_2(I)=1$ . Assume $(A,\mathfrak m)$ is a two-dimensional excellent normal local domain over an algebraically closed field.

Let $\pi \colon X \to \operatorname {\mathrm {Spec}} A $ be a resolution of singularity with exceptional set $E=\bigcup E_i$ .

Definition 4.1. Let $D\ge 0$ be a cycle on X, and let

$$ \begin{align*} h(D)=\max \left\{h^1(\mathcal O_{B}) \,\bigg| \,B \in \sum \mathbb Z E_i, \; B\ge 0, \; \operatorname{\mathrm{Supp}} (B)\subset \operatorname{\mathrm{Supp}} (D)\right\}. \end{align*} $$

We put $h^1(\mathcal O_{B})=0$ if $B=0$ . There exists a unique minimal cycle $C\ge 0$ such that $h^1(\mathcal O_C)=h(D)$ (cf. [30, 4.8]). We call C the cohomological cycle of D. The cohomological cycle of E is denoted by $C_X$ .

Note that $p_g(A)=h(E)$ , and that if A is Gorenstein and $\pi $ is the minimal resolution, then the canonical cycle $Z_{K_X}=C_X$ (see [30, 4.20]). Clearly, the minimally elliptic cycle is the cohomological cycle of itself.

Remark 4.2. (1) If $C_1$ and $C_2$ are cohomological cycles of some cycles on X such that $C_1 \le C_2$ and $h^1(\mathcal O_{C_1})<h^1(C_2)$ , then $\operatorname {\mathrm {Supp}}(C_1) \ne \operatorname {\mathrm {Supp}}(C_2)$ .

(2) In general, for $q<p_g(A)$ , cohomological cycle C with $h^1(\mathcal O_C)=q$ is not unique. For example, there exists a singularity whose minimal good resolution has two minimally elliptic cycles (e.g., [20]).

The following result is a generalization of [25, 2.6].

Proposition 4.3. Assume that $p_g(A)>0$ , and let $D\ge 0$ be a reduced cycle on X. Then the cohomological cycle C of D is the minimal cycle such that $H^0(X\setminus D, \mathcal O_X(K_X))=H^0(X,\mathcal O_X(K_X+C))$ . Therefore, if $g\:X'\to X$ is the blowing-up at a point in $\operatorname {\mathrm {Supp}} C$ and $E'$ the exceptional set for g, then the cohomological cycle $C'$ of $g^*D$ satisfies that $g_*^{-1}C \le C' \le g^*C-E'$ and $h^1(\mathcal O_{C'})=h^1(\mathcal O_C);$ we have $C'=g^*C-E'$ if $\mathcal O_X(K_X+C)$ is generated at the center of the blowing-up.

Proof. Let $F>0$ be an arbitrary cycle with $\operatorname {\mathrm {Supp}}(F)\subset D$ . By the duality, we have $h^1(\mathcal O_F)=h^0( \mathcal {O}_F(K_X+F))$ . From the exact sequence

$$ \begin{align*} 0 \to \mathcal O_X(K_X) \to \mathcal O_X(K_X+F) \to \mathcal O_F(K_X+F) \to 0 \end{align*} $$

and the Grauert–Riemenschneider vanishing theorem, we have

(4.1) $$ \begin{align} h^1(\mathcal O_F)=\ell_A(H^0(X, \mathcal O_X(K_X+F))/H^0(X,\mathcal O_X(K_X))). \end{align} $$

On the other hand, we have the inclusion

$$ \begin{align*} H^0(X, \mathcal O_X(K_X+F)) \subset H^0(X\setminus D, \mathcal O_X(K_X)), \end{align*} $$

where the equality holds if F is sufficiently large; if the equality holds, we obtain $h^1(\mathcal O_F)=h(D)$ , because the upper bound $\ell _A(H^0(X\setminus D, \mathcal O_X(K_X))/H^0(X,\mathcal O_X(K_X)))$ for $h^1(\mathcal O_F)$ depends only on $\operatorname {\mathrm {Supp}}(D)$ . Clearly, the minimum of such cycles F exists as the maximal poles of rational forms in $H^0(X\setminus D, \mathcal O_X(K_X))$ . Let $D'=g^{-1}(D)$ . Since $K_{X'}+g^*C-E'=g^*(K_X+C)$ , we have

$$ \begin{align*} H^0(X', \mathcal O_{X'}(K_{X'}+g^*C-E')) = H^0(X'\setminus D', \mathcal O_X(K_{X'})). \end{align*} $$

Hence, $C' \le g^*C-E'$ . The inequality $g_*^{-1}C \le C'$ is clear. From (4.1), we have $h^1(\mathcal O_{C'})=h^1(\mathcal O_C)$ . If $\mathcal O_X(K_X+C)$ is generated at the center of the blowing-up, then $\mathcal O_{X'}(K_{X'}+g^*C-E')$ has no fixed components, and the minimality of the cycle $g^*C-E'$ follows.

Definition 4.4. We define a reduced cycle $Z^{\bot }$ to be the sum of the components $E_i\subset E$ such that $ZE_i=0$ .

From [24, 3.4], we have the following.

Proposition 4.5. Let $I=I_Z$ be represented by a cycle Z on X and denote by C the cohomological cycle of $Z^{\bot }$ . Assume $\bar {r}(I)=2$ , then $\mathcal O_C(-Z)\cong \mathcal O_C$ and $h^1(\mathcal O_C)=q(I)$ .

The converse of the result above is described as follows.

Proposition 4.6. If C is the cohomological cycle of a cycle on X with $h^1(\mathcal O_C)=q>0$ , then there exist a resolution $Y\to \operatorname {\mathrm {Spec}} A$ and a cycle $Z>0$ on Y such that $\mathcal O_Y(-Z)$ is generated and $q(I_Z)=q(\infty I_Z)=q$ .

Proof. There exists a cycle W on X such that $WE_i<0$ for all $E_i$ and $\mathcal O_X(-W)$ is generated (cf. the proof of [23, 4.5]). Let $h\in I_W$ be a general element. First, we show that there exist a resolution $Y\to \operatorname {\mathrm {Spec}} A$ and a cohomological cycle D on Y with $h^1(\mathcal {O}_D)=q$ such that if $Z_h$ is the exceptional part of $\operatorname {\mathrm {div}}_Y(h)$ , then $Z_h^{\bot }=D_{red}$ . We obtain the resolution Y from X by taking blowing-ups appropriately as follows. Let $H\subset X$ be an irreducible component of the proper transform of $\operatorname {\mathrm {div}}_{\operatorname {\mathrm {Spec}} A}(h)$ intersecting C at a point p, and let $g\:X'\to X$ be the blowing-up at p. Let $C'$ be the cohomological cycle of $g^*C$ . Then $h^1(\mathcal O_{C'})=q$ by Proposition 4.3. If the intersection number $C'(g_*^{-1}H)$ is positive, then we take again the blowing-up at the intersection point. By the property of the intersection number of curves and Proposition 4.3, taking blowing-ups in this manner, we obtain a resolution $Y\to \operatorname {\mathrm {Spec}} A$ and a cohomological cycle D which satisfy the conditions described above; in fact, for an exceptional prime divisor F on Y, we have that $F\le Z_h^{\bot }$ if and only if F does not intersect the proper transform of $\operatorname {\mathrm {div}}_{\operatorname {\mathrm {Spec}} A}(h)$ . Thus, it follows from [22, 3.6] (cf. [24, 3.4]) that $\mathcal O_Y(-nZ_h)$ is generated and $h^1(\mathcal O_Y(-nZ_h))=q$ for $n\ge p_g(A)$ . Then the cycle $Z:=p_g(A)Z_h$ satisfies the assertion.

Corollary 4.7. There exists a strongly elliptic ideal in A if and only if there exists a cohomological cycle C of a cycle on a resolution $Y\to \operatorname {\mathrm {Spec}} A$ such that $h^1(\mathcal O_C)=p_g(A)-1$ .

Example 4.8. Let C be a nonsingular curve of genus $g\ge 2$ and D an divisor on C with $\deg D>0$ . Let $A= \bigoplus _{n\ge 0} H^0( C, \mathcal O_C( nD))$ , and assume that $a(A)=0$ . Then $p_g(A)=g$ and A has no strongly elliptic ideals because any cycle F on any resolution has $h^1(\mathcal O_F)=0$ or g. More precisely, if $Z E_0 = 0$ , where $E_0\subset E$ denotes the curve of genus g, then $I_Z$ is a $p_g$ -ideal; otherwise, $q(\infty I_Z)=0$ .

Next example shows that there are local normal Gorenstein domains that always have strongly elliptic ideals.

Example 4.9. Let C be a nonsingular curve of genus $g\ge 2$ , and put

$$ \begin{align*} A=\bigoplus_{n\ge 0}H^0(\mathcal O_C(nK_C)). \end{align*} $$

Then A is a normal Gorenstein ring by [39]. Suppose that $f: X\to \operatorname {\mathrm {Spec}} A$ is the minimal resolution. We have

$$ \begin{align*} p_g(A)=\sum_{n\ge 0}h^1(\mathcal O_C(nK_C))=g+1 \end{align*} $$

by Pinkham’s formula [28], $E\cong C$ , $\mathcal O_E(-E)\cong \mathcal O_E(K_E)$ , and $K_X=-2E$ (cf. [23, 4.6]). Let $Y\to X$ be the blowing-up at a point $p\in E$ , and let $E_1$ be the fiber of p and $E_0$ the proper transform of E. By Proposition 4.3, we have $C_Y=2E_0+E_1$ . It follows from (b) of the theorem in [30, 4.8] that $h^1(\mathcal O_{E_0})\le h^1(\mathcal O_{nE_0})<p_g(A)$ for every $n\ge 1$ . Hence, the cohomological cycle of $E_0$ is $E_0$ and $h^1(\mathcal O_{E_0})=g=p_g(A)-1$ . Therefore, A has a strongly elliptic ideal by Corollary 4.7.

Next, we construct a strongly elliptic ideal. Take a general linear form $L\in A_1\subset A$ , and suppose that $\sup (\operatorname {\mathrm {div}}_X(L)-E)\cap E$ consists of $\deg K_C$ points $p_1, \dots , p_{2g-2} \in E$ . Let $\phi : X'\to X$ be the blowing-up at $\{p_1, \dots , p_{2g-2}\}$ , and let $F_0$ be the proper transform of E and $F_i=\pi ^{-1}(p_i)$ . Let $Z=F_0+2(F_1+\cdots +F_{2g-2})$ . Then $\mathcal O_{X'}(-Z)$ is generated, $ZC_{X'}\ne 0$ , and $ZF_0=0$ . Thus, $q(I_Z)=g=p_g(A)-1$ (cf. [24, 3.4]). Moreover, we have that $\ell _A(A/I_Z)=g$ by Theorem 2.2 and $I_Z=\overline {\mathfrak m^2}+(L)$ . Note that if C is not hyperelliptic, then $\mathfrak m^2$ is normal, because A is a standard graded ring.