Throughout, ‘link’ means ‘oriented link in S3’, and ‘polynomial’ means ‘Laurent polynomial’. Let L be a link; then 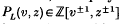 denotes the oriented polynomial of L (see [2, 8]), written in Morton's variables (see [5]), and
denotes the oriented polynomial of L (see [2, 8]), written in Morton's variables (see [5]), and 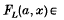
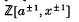 denotes the semi-oriented polynomial of L (see [3]). Let L have components K1, …, Kn. The total linking of L, denoted t(L), is the sum of the linking numbers lk (Ki, Kj) with 1 ≤ i < j ≤ n. Let f be a framing of L (that is, f assigns an integer to each Ki); then f(L) denotes the total framing of L (that is, the sum of these integers), and A(L, f) denotes the naturally associated union of annuli embedded in S3 Define the framed polynomial {L, f} (v, z) to be (–1)n plus (v−1–v)z−1 times the sum, over all non-empty sublinks K of L, of
denotes the semi-oriented polynomial of L (see [3]). Let L have components K1, …, Kn. The total linking of L, denoted t(L), is the sum of the linking numbers lk (Ki, Kj) with 1 ≤ i < j ≤ n. Let f be a framing of L (that is, f assigns an integer to each Ki); then f(L) denotes the total framing of L (that is, the sum of these integers), and A(L, f) denotes the naturally associated union of annuli embedded in S3 Define the framed polynomial {L, f} (v, z) to be (–1)n plus (v−1–v)z−1 times the sum, over all non-empty sublinks K of L, of 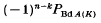 (where K has k components with 1 ≤ k ≤ n).
(where K has k components with 1 ≤ k ≤ n).