Research Article
Automatic continuity with application to C*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 345-347
-
- Article
- Export citation
The Markov branching process with density-independent catastrophes. III. The supercritical case
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 177-192
-
- Article
- Export citation
Front matter
PSP volume 107 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
A new method for generating Bonferroni-type inequalities by iteration
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 601-607
-
- Article
- Export citation
Quasi-standard C*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 349-360
-
- Article
- Export citation
Back matter
PSP volume 107 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
PSP volume 107 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Structure theory for L*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 361-365
-
- Article
- Export citation
Seminorms related to weak compactness and to Tauberian operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 367-375
-
- Article
- Export citation
Back matter
PSP volume 107 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b6
-
- Article
-
- You have access
- Export citation
Research Article
The Schwartz property and nuclearity of spaces of smooth and holomorphic functions in infinite dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 377-385
-
- Article
- Export citation
A lower bound for the Hausdorff dimension of sets of singular n-tuples
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 387-394
-
- Article
- Export citation
A note on stochastic integrators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 395-400
-
- Article
- Export citation
Topological conjugation of Lorenz maps by β-transformations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-413
-
- Article
- Export citation
Corrigendum
Corrigendum
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 415-416
-
- Article
-
- You have access
- Export citation
Front matter
PSP volume 107 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 107 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

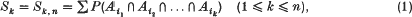
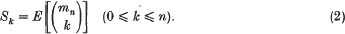
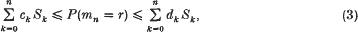
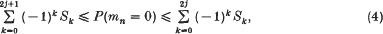
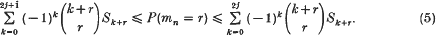
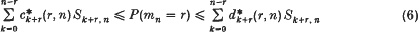
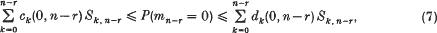
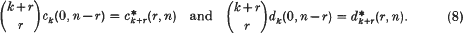
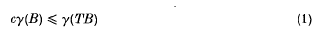
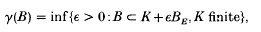
 if and only if the Néron–Severi scheme
if and only if the Néron–Severi scheme  we can replace
we can replace  simply by
simply by  in this case.
in this case.