Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rudolph, Lee
1992.
Topology '90.
p.
343.
Rudolph, Lee
1995.
An obstruction to sliceness via contact geometry and ?classical? gauge theory.
Inventiones Mathematicae,
Vol. 119,
Issue. 1,
p.
155.
Rudolph, Lee
1998.
Quasipositive plumbing (constructions of quasipositive knots and links, V).
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 1,
p.
257.
Rudolph, Lee
1999.
Positive links are strongly quasipositive.
p.
555.
Ferrand, Emmanuel
2001.
On Legendrian knots and polynomial invariants.
Proceedings of the American Mathematical Society,
Vol. 130,
Issue. 4,
p.
1169.
Arnold, V. I.
Bruce, J. W.
Moffatt, H. K.
Pelz, R. B.
and
Goryunov, V. V.
2001.
Plane curves, wavefronts and Legendrian knots.
Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 359,
Issue. 1784,
p.
1497.
Ng, Lenhard
2001.
Maximal Thurston–Bennequin number of two-bridge links.
Algebraic & Geometric Topology,
Vol. 1,
Issue. 1,
p.
427.
NAKAMURA, TAKUJI
2002.
ON CANONICAL GENUS OF FIBERED KNOT.
Journal of Knot Theory and Its Ramifications,
Vol. 11,
Issue. 03,
p.
341.
Rudolph, Lee
2005.
Handbook of Knot Theory.
p.
349.
Ng, Lenhard
2005.
A Legendrian Thurston–Bennequin bound from Khovanov homology.
Algebraic & Geometric Topology,
Vol. 5,
Issue. 4,
p.
1637.
Morton, H R
2007.
Integrality of Homfly 1–tangle invariants.
Algebraic & Geometric Topology,
Vol. 7,
Issue. 1,
p.
327.
KALFAGIANNI, E.
and
LIN, XIAO-SONG
2007.
SEIFERT SURFACES, COMMUTATORS AND VASSILIEV INVARIANTS.
Journal of Knot Theory and Its Ramifications,
Vol. 16,
Issue. 10,
p.
1295.
Ng, Lenhard
2008.
A Skein Approach to Bennequin-Type Inequalities.
International Mathematics Research Notices,
Vol. 2008,
Issue. ,
Kálmán, Tamás
2008.
Rulings of Legendrian knots as spanning surfaces.
Pacific Journal of Mathematics,
Vol. 237,
Issue. 2,
p.
287.
GRUBER, HERMANN
2009.
On knot polynomials of annular surfaces and their boundary links.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 147,
Issue. 1,
p.
173.
MORTON, H. R.
and
RYDER, N. D. A.
2010.
Relations between Kauffman and Homfly satellite invariants.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 149,
Issue. 1,
p.
105.
Paul, Chandrima
Borhade, Pravina
and
Ramadevi, P.
2010.
Composite representation invariants and unoriented topological string amplitudes.
Nuclear Physics B,
Vol. 841,
Issue. 3,
p.
448.
Mariño, Marcos
2010.
String Theory and the Kauffman Polynomial.
Communications in Mathematical Physics,
Vol. 298,
Issue. 3,
p.
613.
Cornwell, C. R.
2011.
Bennequin Type Inequalities in Lens Spaces.
International Mathematics Research Notices,
NG, LENHARD
2012.
ON ARC INDEX AND MAXIMAL THURSTON–BENNEQUIN NUMBER.
Journal of Knot Theory and Its Ramifications,
Vol. 21,
Issue. 04,
p.
1250031.
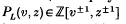 denotes the oriented polynomial of L (see [2, 8]), written in Morton's variables (see [5]), and
denotes the oriented polynomial of L (see [2, 8]), written in Morton's variables (see [5]), and 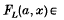
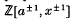 denotes the semi-oriented polynomial of L (see [3]). Let L have components K1, …, Kn. The total linking of L, denoted t(L), is the sum of the linking numbers lk (Ki, Kj) with 1 ≤ i < j ≤ n. Let f be a framing of L (that is, f assigns an integer to each Ki); then f(L) denotes the total framing of L (that is, the sum of these integers), and A(L, f) denotes the naturally associated union of annuli embedded in S3 Define the framed polynomial {L, f} (v, z) to be (–1)n plus (v−1–v)z−1 times the sum, over all non-empty sublinks K of L, of
denotes the semi-oriented polynomial of L (see [3]). Let L have components K1, …, Kn. The total linking of L, denoted t(L), is the sum of the linking numbers lk (Ki, Kj) with 1 ≤ i < j ≤ n. Let f be a framing of L (that is, f assigns an integer to each Ki); then f(L) denotes the total framing of L (that is, the sum of these integers), and A(L, f) denotes the naturally associated union of annuli embedded in S3 Define the framed polynomial {L, f} (v, z) to be (–1)n plus (v−1–v)z−1 times the sum, over all non-empty sublinks K of L, of 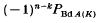 (where K has k components with 1 ≤ k ≤ n).
(where K has k components with 1 ≤ k ≤ n).