Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-07T02:54:05.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Probabilistic factorization of a quadratic matrix polynomial

Published online by Cambridge University Press:  24 October 2008

Joanne Kennedy  and
David Williams
Joanne Kennedy
Affiliation:
Statistical Laboratory, 16 Mill Lane, Cambridge CB2 1SB
David Williams
Affiliation:
Statistical Laboratory, 16 Mill Lane, Cambridge CB2 1SB
Get access Rights & Permissions [Opens in a new window]

Extract

A purely algebraic result. We begin by stating the following theorem. Theorem. Let E be a finite set, and let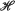denote the set of real E × E matrices with non-negative off-diagonal elements and with non-positive row sums. Let A be a symmetric element of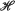, and let V be a diagonal real E × E matrix. Then there exists a unique pair (H+, H−) of elements of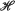such that

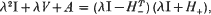
I denoting the identity E × E matrix, and the superscript T signifying transpose. It is an immediate consequence that

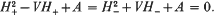
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 107 , Issue 3 , May 1990 , pp. 591 - 600
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barlow, M. T., Rogers, L. C. G. and Williams, D.. Wiener–Hopf factorization for matrices. In Séminaire de Probabilités XIV, Lecture Notes in Math. vol. 784 (Springer-Verlag, 1980), pp. 324–331.Google Scholar
[2]Clancey, K. and Gohberg, I. C.. Factorization of Matrix Functions and Singular Integral Operators. Operator Theory: Advances and Applications, vol. 3 (Birkhäuser, 1981).CrossRefGoogle Scholar
[3]Gohberg, I. C. and Krein, M. G.. Introduction to the Theory of Linear Non-selfadjoint Operators. Translation of Math. Monographs, vol. 18 (American Mathematical Society, 1969).Google Scholar
[4]London, R. R., McKean, H. P., Rogers, L. C. G. and Williams, D.. A martingale approach to some Wiener–Hopf problems. II. In Séminaire de Probabilités XVI, Lecture Notes in Math. vol. 920 (Springer-Verlag, 1982), pp. 68–90.CrossRefGoogle Scholar
[5]Williams, D.. A ‘potential-theoretic’ note on the quadratic Wiener–Hopf equation for matrices. In Séminaire de Probabilités XVI, Lecture Notes in Math. vol. 920 (Springer-Verlag, 1982), pp. 91–94.CrossRefGoogle Scholar