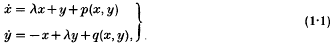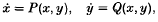Research Article
One-relator surface groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 467-474
-
- Article
- Export citation
Homotopy skein modules of orientable 3-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 475-488
-
- Article
- Export citation
Quantum groups and representations of monoidal categories
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 261-290
-
- Article
- Export citation
On ideals and sublattices in linear lattices and F-lattices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-87
-
- Article
- Export citation
A calculus for rational tangles: applications to DNA recombination
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 489-515
-
- Article
- Export citation
Degenerate curves and harmonic analysis
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 89-96
-
- Article
- Export citation
Localization of seif-homotopy equivalences inducing the identity on homology
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-297
-
- Article
- Export citation
Orientable surfaces in the 4-sphere associated with non-orientable knotted surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 299-306
-
- Article
- Export citation
The sum of Rademacher functions and Hausdorff dimension
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 97-103
-
- Article
- Export citation
Characteristic classes of Galois representations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 517-522
-
- Article
- Export citation
The Hausdorff dimension of certain sets of singular n-tuples
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 105-110
-
- Article
- Export citation
Copies of l∞ in an operator space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 523-526
-
- Article
- Export citation
Periodic orbits and fixed points of a C1 orientation-preserving embedding of D2
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-310
-
- Article
- Export citation
The uniform compactification of a locally compact abelian group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 527-538
-
- Article
- Export citation
A Markov chain identity and monotonicity of the diffusion constants for a random walk in a heterogeneous environment
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-126
-
- Article
- Export citation
Character-pure locally compact abelian groups and their dual groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 311-315
-
- Article
- Export citation
Annihilators in JB-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 317-323
-
- Article
- Export citation
Toeplitz operators associated with analytic crossed products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 539-549
-
- Article
- Export citation
Word problems related to periodic solutions of a non-autonomous system
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-151
-
- Article
- Export citation
Three-dimensional constitutive equations for rigid/perfectly plastic granular materials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-169
-
- Article
- Export citation

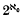 in every infinite-dimensional
in every infinite-dimensional 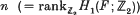 is even (ef. [
is even (ef. [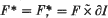 is a closed connected genus
is a closed connected genus 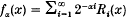 for 0 ≤ x < 1, where
for 0 ≤ x < 1, where 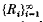 is the sequence of Rademacher functions. We give a class of
is the sequence of Rademacher functions. We give a class of 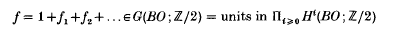
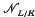 denote the multiplicative transfer (see e.g. [3,
denote the multiplicative transfer (see e.g. [3,