Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Patzschke, N.
and
Zähle, M.
1993.
Fractional differentiation in the self-affine case. III. The density of the Cantor set.
Proceedings of the American Mathematical Society,
Vol. 117,
Issue. 1,
p.
137.
Hu, Tian-You
1997.
The local dimensions of the Bernoulli convolution associated with the golden number.
Transactions of the American Mathematical Society,
Vol. 349,
Issue. 7,
p.
2917.
Hunt, Brian
1998.
The Hausdorff dimension of graphs of Weierstrass functions.
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 3,
p.
791.
Heurteaux, Yanick
2003.
Weierstrass functions with random phases.
Transactions of the American Mathematical Society,
Vol. 355,
Issue. 8,
p.
3065.
Feng, De-Jun
2005.
The limited Rademacher functions and Bernoulli convolutions associated with Pisot numbers.
Advances in Mathematics,
Vol. 195,
Issue. 1,
p.
24.
Liang, Yongshun
2009.
On the fractional calculus of Besicovitch function.
Chaos, Solitons & Fractals,
Vol. 42,
Issue. 5,
p.
2741.
LIANG, Y. S.
2017.
DEFINITION AND CLASSIFICATION OF ONE-DIMENSIONAL CONTINUOUS FUNCTIONS WITH UNBOUNDED VARIATION.
Fractals,
Vol. 25,
Issue. 05,
p.
1750048.
WU, YIPENG
YAO, KUI
and
ZHANG, XIA
2018.
THE HADAMARD FRACTIONAL CALCULUS OF A FRACTAL FUNCTION.
Fractals,
Vol. 26,
Issue. 03,
p.
1850025.
Zhu, Yahui
and
Xiao, Wei
2019.
The classification of functions of unbounded variation on closed intervals.
p.
2023.
LIANG, YONG-SHUN
2019.
PROGRESS ON ESTIMATION OF FRACTAL DIMENSIONS OF FRACTIONAL CALCULUS OF CONTINUOUS FUNCTIONS.
Fractals,
Vol. 27,
Issue. 05,
p.
1950084.
WANG, BIN
JI, WENLONG
ZHANG, LEGUI
and
LI, XUAN
2020.
THE RELATIONSHIP BETWEEN FRACTAL DIMENSIONS OF BESICOVITCH FUNCTION AND THE ORDER OF HADAMARD FRACTIONAL INTEGRAL.
Fractals,
Vol. 28,
Issue. 07,
p.
2050128.
Yuan, Xixi
and
Cai, Zhanchuan
2021.
A Generalized Walsh System and Its Fast Algorithm.
IEEE Transactions on Signal Processing,
Vol. 69,
Issue. ,
p.
5222.
PAN, YUEWEI
and
YI, SHANFENG
2023.
OSCILLATORY PROPERTY AND DIMENSIONS OF RADEMACHER SERIES.
Fractals,
Vol. 31,
Issue. 05,
Liang, Yong Shun
and
Su, Wei Yi
2024.
A Geometric Based Connection between Fractional Calculus and Fractal Functions.
Acta Mathematica Sinica, English Series,
Vol. 40,
Issue. 2,
p.
537.
Yi, Shanfeng
2025.
Fractal dimensions of the graph and level sets of the Riemann-Rademacher functions.
Monatshefte für Mathematik,
Vol. 206,
Issue. 3,
p.
747.


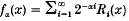 for 0 ≤ x < 1, where
for 0 ≤ x < 1, where 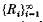 is the sequence of Rademacher functions. We give a class of
is the sequence of Rademacher functions. We give a class of 