Published online by Cambridge University Press: 24 October 2008
The main aim of this paper is to study the role of the assumptions in the following
Theorem 0. Every ideal I of codimension 1 in an F-lattice X is closed†.
For X a Banach lattice this result appears in [11], ii.5·3, corollary 3. The proof carries over to the case where X is an. F-lattice, i.e. a topological linear lattice the topology of which is metrizable and complete, with the help of a result due to Klee ([10], theorem v.5·5; see also [3], theorem 16·6). We first note that the assumption of metric completeness is essential (Example 2). We then extend Theorem 0 to the case of ideals of finite codimension (Theorem 1), and show that non-closed ideals exist whenever X is infinite-dimensional (Corollary 2). Our main result commenting on Theorem 0 is, however, the existence of dense sublattices of arbitrary codimension between 1 and 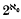 in every infinite-dimensional F-lattice (Theorem 6).
in every infinite-dimensional F-lattice (Theorem 6).