Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T01:08:04.858Z Has data issue: false hasContentIssue false
  • English
  • Français

The uniform compactification of a locally compact abelian group

Published online by Cambridge University Press:  24 October 2008

M. Filali
M. Filali
Affiliation:
Department of Mathematics, University of Sheffield
Get access Rights & Permissions [Opens in a new window]

Extract

In recent years, the Stone-Čech compactification of certain semigroups (e.g. discrete semigroups) has been an interesting semigroup compactification (i.e. a compact right semitopological semigroup which contains a dense continuous homomorphic image of the given semigroup) to study, because an Arens-type product can be introduced. If G is a non-compact and non-discrete locally compact abelian group, then it is not possible to introduce such a product into the Stone-Čech compactification βG of G (see [1]). However, let UC(G) be the Banach algebra of bounded uniformly continuous complex functions on G, and let UG be the spectrum of UC(G) with the Gelfand topology. If f∈ UC(G), then the functions f and fy defined on G by

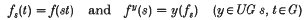
are also in UC(G).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 108 , Issue 3 , November 1990 , pp. 527 - 538
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baker, J. W. and Butcher, R. J.. The Stone-Čech compactification of a topological semigroup. Math. Proc. Cambridge Philos. Soc. 80 (1976), 103–107.CrossRefGoogle Scholar
[2]Baker, J. W. and Milnes, P.. The ideal structure of the Stone-Čech compactification of a group. Math. Proc. Cambridge Philos. Soc. 82 (1977), 401–409.CrossRefGoogle Scholar
[3]Berglund, J. F., Junghenn, H. D. and Milnes, P.. Compact Right Topological Semigroups and Generalisations of Almost Periodicity. Lecture Notes in Math. vol. 663 (Springer-Verlag, 1978).CrossRefGoogle Scholar
[4]Burckel, R. B.. Weakly Almost Periodic Functions on Semigroups (Gordon and Breach, 1970).Google Scholar
[5]Butcher, R. J.. The Stone-Cech compactification of a topological semigroup and its algebra of measures. Ph.D. thesis, University of Sheffield (1975).Google Scholar
[6]Filali, M.. An Arens-type product on the Banach dual of some C*-algebras of bounded continuous functions on a semitopological semigroup. Ph.D. thesis, University of Sheffield (1989).Google Scholar
[7]Gillman, L. and Jerison, M.. Rings of Continuous Functions (Van Nostrand, 1960).CrossRefGoogle Scholar
[8]Hamye, S. M.. Some compactifications of a semitopological semigroup and its algebra of charges. Ph.D. thesis, University of Sheffield (1986).CrossRefGoogle Scholar
[9]Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis, vol. 1 (Springer-Verlag, 1963).Google Scholar
[10]Hindman, N.. Minimal ideals and cancellation in βℕ. Semigroup Forum 25 (1982), 291–310.CrossRefGoogle Scholar
[11]Hindman, N. and Pym, J.. Free groups and semigroups in βℕ. Semigroup Forum 30 (1984), 177–193.CrossRefGoogle Scholar
[12]Parsons, D. J.. The Centre of the second dual of a commutative semigroup algebra. Math. Proc. Cambridge Philos. Soc. 95 (1984), 71–92.CrossRefGoogle Scholar
[13]Ruppert, W.. On semigroup compactifications of topological groups. Proc. Roy. Irish Acad. 79 (1979), 179–200.Google Scholar
[14]Simmons, G. F.. Introduction to Topology and Modern Analysis (McGraw-Hill, 1963).Google Scholar