1. In many problems in theoretical physics one encounters situations in which it is desirable to be able to expand orbitals centred at one particle about another centre, frequently, but not always, another particle.

There have long been available methods for permitting this to be effected for bound states but no such procedures are available for the continuum.

Typical examples of physical situations in which such procedures are desirable are positron scattering from atomic and molecular systems, electron scattering from molecules, and nucleon scattering from light nuclei, to mention only a few.

The author's interest arose from a desire to establish a general theory of slow electron scattering from molecules, and an account of such a theory will appear shortly (1).

A conjecture of Orlov predicts that derived equivalent smooth projective varieties over a field have isomorphic Chow motives. The conjecture is known for curves, and was recently observed for surfaces by Huybrechts. In this paper we focus on threefolds over perfect fields, and unconditionally secure results, which are implied by Orlov's conjecture, concerning the geometric coniveau filtration, and abelian varieties attached to smooth projective varieties.

Singer [7] proved that in a Banach space all basic sequences are shrinking if and only if all of them are boundedly complete. Afterwards; Zippin [2] proved a similar result for Schauder bases, and it was extended [1] to Schauder decompositions.

1.Introduction. To every closed subalgebra S of a regular algebra R(D) of functions tending to zero at infinity on a discrete space D we define the Rudin spectrum of S to be the partition of D consisting of the equivalence classes of the equivalence relation .

The study of the Riccati equation

plays an essential part in the ‘large parameter’ theory of the inhomogeneous van der Pol equation; see for example Littlewood(1), (2). The crucial result is Lemma B of (1), restated and proved as Lemma 5 of (2); for the present paper the relevant parts of it are as follows:

Lemma 1. Let z = z(x) be the solution of (1·1) which satisfies the initial condition z = 0 at x = 0, and assume α > 0. Then there is a unique β0 = β0(α) with the property that

(i) if β > β0 then z → − ∞ as x → + ∞;

(ii) if β < β0 then z → + ∞ at a vertical asymptote x = x0(α,β);

(iii) if β = β0 then z ≥ 0 in 0 ≤ x < + ∞ and z = x + β0 + o(1) as x → + ∞.

Moreover, β0(α) is a continuous monotone increasing function of α.

Recent work of Atiyah (1) on the Grothendieck rings of classifying spaces of finite groups has yielded, among many other interesting results, a spectral sequence relating the simple integer cohomology of a finite group to its representation ring. He has determined the first differential operator of the spectral sequence which affects the p-part of the cohomology, and the question naturally arises, when is it the only non-zero one. My object in this note is to show that this is so for a large class of groups.

A simple expression is derived for the magnetic vector potential of current in a thin ring, in terms of the first derivative of toroidal functions of zero order. The axial and radial field components and the mutual inductance between two wire rings are obtained. These expressions are evaluated on a digital computer and the results are summarized in a series of graphs.

We consider random walks on the mapping class group that have finite first moment with respect to the word metric, whose support generates a non-elementary subgroup and contains a pseudo-Anosov map whose invariant Teichmüller geodesic is in the principal stratum of quadratic differentials. We show that a Teichmüller geodesic typical with respect to the harmonic measure for such random walks, is recurrent to the thick part of the principal stratum. As a consequence, the vertical foliation of such a random Teichmüller geodesic has no saddle connections.

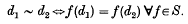
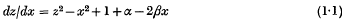
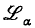For countable admissible α, one can add a new infinitary propositional connective to so that the extended language obeys the Barwise compactness theorem, and the set of valid sentences is complete α-r.e.

Aside from obeying the compactness theorem and a completeness theorem, ordinary finitary predicate calculus is also truth-functionally complete.

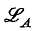In (1), Barwise shows that for countable admissible A, provides a fragment of 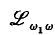which obeys a compactness theorem and a completeness theorem. However, we of course lose truth-functional completeness, with respect to infinitary propositional connectives that operate on infinite sequences of propositional variables. This raises the question of studying extensions of the language obtained by adding infinitary propositional connectives, in connexion with the Barwise compactness and completeness theorems, and other metatheorems, proved for Some aspects of this project are proposed in (3). It is the purpose of this paper to answer a few of the more basic questions which arise in this connexion.

We have not attempted to study the preservation of interpolation or implicit definability. This could be quite interesting if done systematically.

There has lately been an unusual amount of interest in a relativistic phenomenon which has come to be called the clock paradox. It may be simply stated in the following way. If a man were to leave the earth on a powered space ship for an extended trip into space, he would find upon returning to earth that he was younger than he would have been if he had remained on earth.

In a recent publication the problem of determining the abundance of two interacting species of animals was investigated, and the fundamental equations were established.

Introduction. Agarwalin 1953 ((1)) gave the most general transformations involving bilateral cognate trigonometrical series of the hypergeometric type. Later, Shukla in 1957 ((2)) gave certain relations involving the products of two bilateral hypergeometric series. In this paper an attempt has been made to establish certain new transformations involving the products of two and more bilateral hypergeometric type of series. (For notations and definitions see Agarwal ((1)).)

Let p be a prime and let d be a positive integer which divides p−1. Assume that X is a space such that

1. The quadrics of space are linearly dependent on ten among them; any ten linearly independent quadrics may be chosen to constitute the base, but it is customary in analytical work to select the four squares and the six products of pairs of four planes which are the faces of some tetrahedron of reference. This choice is adequate enough for many purposes, but it gives an unsymmetrical twist to the work; whereas four quadrics of the base are repeated planes the other six are plane pairs, and the curve common to two of the ten base quadrics can be a skew quadrilateral, a repeated line-pair, or a line counted four times. This radical defect can be mitigated by taking as base a certain set of ten non-singular quadrics, namely, the set of ten fundamental quadrics which is so prominent a feature of Klein's figure of six mutually apolar linear complexes. Every pair of such a set of ten quadrics has its two members related to one another in precisely the same way; their common curve is a skew quadrilateral and they are their own polar reciprocals with respect to each other.

The paper studies the influence of the electrical conductivity tensor upon the motion of a fluid in a MHD generator, under the conditions shown in our preceding work. The problem is also formulated in terms of the theory of distributions and the system of equations which determines the functions Ψ = ψ + y and φ = ϕ + ϕe depends on two parameters λ and v (= ωτ). Due to the Hall current, the problem is no longer asymmetrical in the variable y, as in the first case, it therefore has to be separated into an asymmetric and a symmetric problem. Developing a method of successive approximations as against two parameters, it can be shown that the exact solution of the problem may be obtained.

Let V be an absolutely irreducible affine variety over $\mathbb{F}_p$. A Lehmer point on V is a point whose coordinates satisfy some prescribed congruence conditions, and a visible point is one whose coordinates are relatively prime. Asymptotic results for the number of Lehmer points and visible points on V are obtained, and the distribution of visible points into different congruence classes is investigated.

We prove that the Poincaré conjecture implies that the 4-dimensional version of the realization theorem for Whitehead torsion is false. We show that infinitely many examples may be constructed to demonstrate this.

This note is a brief excursion into a new theory of modules over a commutative ring R modulo a Serre subcategory S of the category of R-modules, in the sense that the modules of S are regarded as trivial. As a demonstration of the theory we have chosen to extend the primary decomposition theorem for submodules of a Noetherian .R-module from the familiar case of S trivial (i.e. the only R-module of S is the zero module) to the general case.

1. Introduction. The relationship between sufficient statistics and the exponential family was first investigated by Pitman (8) and Koopman (7). The treatments assumed a density function f(x; θ) which was at least differentiable with respect to both arguments.

The usual formula for the rate of loss of energy by a fast particle contains a factor z2, the square of the charge, which might suggest that He+ should lose energy at a quarter of the rate that He++ does. It is shown that when Born's approximation is applicable the energy-loss is reduced instead by a factor of about ⅝.