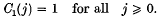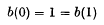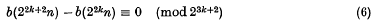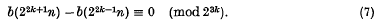Research Article
A commutant property of symmetric ternary algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-4
-
- Article
- Export citation
Extensions of self-dual orders
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-7
-
- Article
- Export citation
J-Equivalence of group representations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 9-14
-
- Article
- Export citation
Regular neighbourhoods and mapping cylinders
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 15-18
-
- Article
- Export citation
On the relation of complex cobordism to connective K-theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-22
-
- Article
- Export citation
A theorem on bounded synthesis
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-26
-
- Article
- Export citation
Lifting convergent sequences with networks
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 27-30
-
- Article
- Export citation
A diophantine problem on groups. III
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-47
-
- Article
- Export citation
A note on the Fourier transform of generalized functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-51
-
- Article
- Export citation
Proof of the Churchhouse conjecture concerning binary partitions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 53-56
-
- Article
- Export citation
On application of a certain formula
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-59
-
- Article
- Export citation
Stochastic monotonicity and queues subject to tidal interruptions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 61-75
-
- Article
- Export citation
On the asymptotic behaviour of solutions of x″ + a(t)f(x) = 0
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 77-88
-
- Article
- Export citation
Physical interpretation of N.U.T. metric
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 89-94
-
- Article
- Export citation
Global results and stability of motion†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 95-102
-
- Article
- Export citation
The propagation of Rayleigh waves over curved surfaces at high frequency
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-121
-
- Article
- Export citation
The downstream solution for steady viscous flow past a paraboloid
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 123-133
-
- Article
- Export citation
A uniformly asymptotic solution for incompressible flow past thin sharp-edged aerofoils at zero incidence
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-155
-
- Article
- Export citation
Internal wave motion in a non-homogeneous viscous fluid of variable depth
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 157-167
-
- Article
- Export citation
Thermostatics of an elastic Cosserat plate containing a circular hole
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 169-174
-
- Article
- Export citation



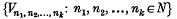
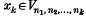
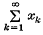
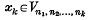
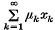
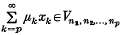
 be a sequence in ĝ, not too slowly growing in a certain precise sense. Then, provided ĝ has ‘not too many’ elements of finite order, the sequences
be a sequence in ĝ, not too slowly growing in a certain precise sense. Then, provided ĝ has ‘not too many’ elements of finite order, the sequences