Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T15:11:23.278Z Has data issue: false hasContentIssue false
  • English
  • Français

Lifting convergent sequences with networks

Published online by Cambridge University Press:  24 October 2008

J. H. Webb
J. H. Webb
Affiliation:
University of cape Town, South Africa
Get access Rights & Permissions [Opens in a new window]

Extract

Definition (Moukoko Priso(2)). A locally convex spaceE[T] is said to have a strict absorbent network of type Σ if there exists in E a family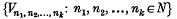of absolutely convex absorbent sets such that

(1) if {nk} is a sequence of positive integers and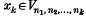for each k, then the series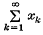converges in E[T]

(2) for each sequence {nk} there is a sequence {λk} of positive real numbers such that, if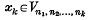and 0 ≤ μk ≤ λkfor each k, then

(i) 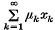converges in E[T], and

(ii) 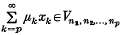for each p.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 70 , Issue 1 , July 1971 , pp. 27 - 30
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Husain, T.The open mapping and closed graph theorems in topological vector spaces (Oxford, 1965)CrossRefGoogle Scholar
(2)Moukoko Priso, P.Sur les questions de relèvement de suites convergentes. C.R. Acad. Sci., Paris, Sér. A 269 (1969), 1063–1065.Google Scholar
(3)de Wilde, M.Réseaux dans les espaces linéaires à semi-normes. Mem. Soc. Roy. Sci. Liège 17 (1969).Google Scholar