Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rindler, Harald
1976.
Gleichverteilte Folgen in lokalkompakten Gruppen.
Monatshefte für Mathematik,
Vol. 82,
Issue. 3,
p.
207.
Lyons, Russell
1986.
The measure of non-normal sets.
Inventiones Mathematicae,
Vol. 83,
Issue. 3,
p.
605.
Lyons, Russell
2020.
The Journal of Fourier Analysis and Applications.
p.
363.


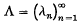 be a sequence in ĝ, not too slowly growing in a certain precise sense. Then, provided ĝ has ‘not too many’ elements of finite order, the sequences
be a sequence in ĝ, not too slowly growing in a certain precise sense. Then, provided ĝ has ‘not too many’ elements of finite order, the sequences