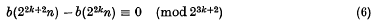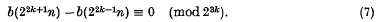Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hirschhorn, M. D.
and
Loxton, J. H.
1975.
Congruence properties of the binary partition function.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 78,
Issue. 3,
p.
437.
Reznick, Bruce
1990.
Analytic Number Theory.
Vol. 85,
Issue. ,
p.
451.
Rødseth, Øystein J.
and
Sellers, James A.
2002.
Binary Partitions Revisited.
Journal of Combinatorial Theory, Series A,
Vol. 98,
Issue. 1,
p.
33.
Gawron, Maciej
Miska, Piotr
and
Ulas, Maciej
2018.
Arithmetic properties of coefficients of power series expansion of
$$\prod _{n=0}^{\infty }\left( 1-x^{2^{n}}\right) ^{t}$$
∏
n
=
0
∞
1
-
x
2
n
t
(with an appendix by Andrzej Schinzel).
Monatshefte für Mathematik,
Vol. 185,
Issue. 2,
p.
307.
Ulas, Maciej
and
Żmija, Błażej
2019.
On arithmetic properties of binary partition polynomials.
Advances in Applied Mathematics,
Vol. 110,
Issue. ,
p.
153.
Ulas, Maciej
and
Żmija, Błażej
2019.
On p-adic valuations of colored p-ary partitions.
Monatshefte für Mathematik,
Vol. 188,
Issue. 2,
p.
351.
Ulas, Maciej
2019.
2-Adic valuations of coefficients of certain integer powers of formal power series.
International Journal of Number Theory,
Vol. 15,
Issue. 04,
p.
723.
Żmija, Błażej
2020.
Recurrence sequences connected with the m–ary partition function and their divisibility properties.
Journal of Number Theory,
Vol. 211,
Issue. ,
p.
322.
Ulas, Maciej
and
Żmija, Błażej
2021.
On p-adic valuations of certain m colored p-ary partition functions.
The Ramanujan Journal,
Vol. 55,
Issue. 2,
p.
623.
Sobolewski, Bartosz
and
Ulas, Maciej
2023.
Values of Binary Partition Function Represented by a Sum of Three Squares.
Results in Mathematics,
Vol. 78,
Issue. 5,