Reviews
Obras completas, by Kurt Gödel. Edited by Jesús Mosterín. Alianza universidad. Alianza Editorial, Madrid1981, 430 pp. - Jesús Mosterín. Prólogo. Pp. 9–13. - Jesús Mosterín. Introducción. Pp. 15–19, 35–36, 41, 45–54, 91, 95–96, 101–102, 105–106, 109, 113–114, 117–119, 127–129, 147–150, 183–184, 187–188, 191, 195–196, 205–213, 295–296, 329–330, 337–339, 401–403, 413–414. - Kurt Gödel. La suftciencia de los axiomas del caĺculo lógico de primer orden. Pp. 20–34. Spanish translation by Jesús Mosterín of 4182. - Kurt Gödel. Un caso especial del problema de la decision en la Idgica tedrica. Pp. 37–39. Spanish translation by Jesús Mosterín of 4187. - Kurt Gödel. Algunos resultados metamatemáticos sobre completudy consistencia. Pp. 42–43. Spanish translation by Jesús Mosterín of 4181. - Kurt Gödel. Sobre sentencias formalmente indecidibles de Principia mathematica y sistemas afines. Pp. 55–89. Spanish translation by Jesús Mosterín of 4185 with an added note from XXXVII 405(5). - Kurt Gödel. Sobre completud y consistencia. Pp. 92–94. Spanish translation by Jesús Mosterin of 4188 with an added note from XXXVII 405(6). - Kurt Gödel. Discusión sobre la fundamentación de la matemática. Pp. 97–100. Spanish translation by Jesús Mosterín of 4184 and 4185. - Kurt Gödel. Una propriedad de los modelos del cálculo conectivo. Pp. 103–104. Spanish translation by Jesús Mosterín of 4189.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1199-1201
-
- Article
- Export citation
L. E. J. Brouwer. Brouwer's Cambridge lectures on intuitionism. Edited by D. van Dalen. Cambridge University Press, Cambridge, New York, Melbourne, etc., 1981, xii + 109 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 214-215
-
- Article
- Export citation
Research Article
Closure properties of almost-finiteness classes in recursive function theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 756-763
-
- Article
- Export citation
Reviews
Haim Gaifman. Models and types of Peano's arithmetic. Annals of mathematical logic, vol. 9(1976), pp. 223–306. - Julia F. Knight. Omitting types in set theory and arithmetic. The journal of symbolic logic, vol. 41 (1976), pp. 25–32. - Julia F. Knight. Hanf numbers for omitting types over particular theories. The journal of symbolic logic, vol. 41 (1976), pp. 583–588. - Fred G. Abramson and Leo A. Harrington. Models without indiscernibles. The journal of symbolic logic, vol. 41 (1976), vol. 43 (1978), pp. 572–600.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 484-485
-
- Article
- Export citation
Research Article
Notions of weak genericity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 764-770
-
- Article
- Export citation
Reviews
Neil Tennant. Natural logic. Edinburgh University Press, Edinburgh1978, ix + 196 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 215-217
-
- Article
- Export citation
Kit Fine. Failures of the interpolation lemma in quantified modal logic. The journal of symbolic logic, vol. 44, (1979), pp. 201–206.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 486-488
-
- Article
- Export citation
M. P. Fourman and D. S. Scott. Sheaves and logic. Applications of sheaves, Proceedings of the Research Symposium on Applications of Sheaf Theory to Logic, Algebra, and Analysis, Durham, July 9–21, 1977, edited by M. P. Fourman, C. J. Mulvey, and D. S. Scott, Lecture notes in mathematics, vol. 753, Springer-Verlag, Berlin, Heidelberg, and New York, 1979, pp. 302–401.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1201-1203
-
- Article
- Export citation
Detlef Laugwitz. Infinitesimalkalkül. Kontinuum und Zahlen—eine elementare Einführung in die Nichtstandard-Analysis. Bibliographisches Institut, Mannheim, Vienna, and Zürich, 1978, 187 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 217-219
-
- Article
- Export citation
Edward Nelson. Internal set theory: a new approach to nonstandard analysis. Bulletin of the American Mathematical Society, vol. 83 (1977), pp. 1165–1198.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1203-1204
-
- Article
- Export citation
Research Article
A weak absolute consistency proof for some systems of illative combinatory logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 771-776
-
- Article
- Export citation
Reviews
S. K. Thomason. Noncompactness in propositional modal logic. The journal of symbolic logic, vol. 37 no. 4 (for 1972, pub. 1973), pp. 716–720. - Kit Fine. An incomplete logic containing S4. Theoria, vol. 40 (1974), pp. 23–29. - S. K. Thomason. An incompleteness theorem in modal logic. Theoria, vol. 40 (1974), pp. 30–34. - Martin Gerson. The inadequacy of the neighbourhood semantics for modal logic. The journal of symbolic logic, vol. 40 (1975), pp. 141–148. - Martin Sebastian Gerson. An extension of S4 complete for the neighbourhood semantics but incomplete for the relational semantics. Studio logica, vol. 34 (1975), pp. 333–342. - Martin Gerson. A neighbourhood frame for T with no equivalent relational frame. Zeitschrift für mathematische Logik und Grundlugen der Mathematik, vol. 22 (1976), pp. 29–34. - V. B. Šehtman. On incomplete propositional logics. Soviet mathematics, vol. 18 (1977), pp. 985–989. (English translation by B. F. Wells of O népolnyh logikah vyskazyvanij, Doklady Akadémii Nauk SSSR, vol. 235 (1977), pp. 542–545.) - J. F. A. K. van Benthem. Two simple incomplete modal logics. Theoria, vol. 44 (1978), pp. 25–37. - J. F. A. K. van Benthem and W. J. Blok. Transitivity follows from Dummett's axiom. Theoria, vol. 44 (1978), pp. 117–118. - J. F. A. K. van Benthem. Syntactic aspects of modal incompleteness theorems. Theoria, vol. 44 (1978), vol. 45 (1979). pp. 63–77.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 488-495
-
- Article
- Export citation
Tyler Burge. Frege and the hierarchy. Synthese, vol. 40 (1979), pp. 265–281. - Terence D. Parsons. Frege's hierarchies of indirect senses and the paradox of analysis. The foundations of analytic philosophy, edited by Peter A. French, Theodore E. UehlingJr., and Howard K. Wettstein, Midwest studies in philosophy, vol. 6, University of Minnesota Press, Minneapolis1981, pp. 37–57.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 495-496
-
- Article
- Export citation
J. Zucker. The correspondence between cut-elimination and normalization. Annals of mathematical logic, vol. 7 no. 1 (1974), pp. 1–112, and vol. 7, no. 2–3 (1974), pp. 113–156.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1204-1206
-
- Article
- Export citation
Research Article
Sentences implying their own provability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 777-789
-
- Article
- Export citation
Reviews
Klaus Potthoff. Einführung in die Modelltheorie und ihre Anwendungen. Wissenschaftliche Buchgesellschaft, Darmstadt1981, pp. XII + 277 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 219-220
-
- Article
- Export citation
G. L. Cherlin. The model-companion of a class of structures. The journal of symbolic logic, vol. 37 (1972), pp. 546–556. - L. Lipshitz and D. Saracino. The model companion of the theory of commutative rings without nilpotent elements. Proceedings of the American Mathematical Society, vol. 38 (1973), pp. 381–387. - Angus Macintyre. Model-completeness for sheaves of structures. Fundamenta mathematicae, vol. 81 no. 1 (1973), pp. 73–89.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 496
-
- Article
- Export citation
Andrzej Grzegorczyk. An outline of mathematical logic. Fundamental results and notions explained with all details. English translation by Olgierd Wojtasiewicz and Wacław Zawadowski of the second edition of Zarys logiki matematycznej. Synthese library, vol. 70. D. Reidel Publishing Company, Dordrecht and Boston, and PWN—Polish Scientific Publishers, Warsaw, 1974, X + 596 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 220-222
-
- Article
- Export citation
Paul-Henri Steinauer. La logique au service du droit. Étude de logique contemporaine pour une meilleure communication de la pensée juridique. Arbeiten aus dem Iuristischen Seminar der Universitat Freiburg Schweiz, no. 48. Éditions Universitaires Fribourg Suisse, Fribourg1979, XII + 198 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1206-1207
-
- Article
- Export citation
Research Article
Intermediate β-r.e. degrees and the half-jump
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 790-796
-
- Article
- Export citation

 bea. class of subsets of
bea. class of subsets of 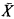 simple};
simple};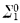 sentence
sentence 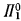 would work. In that case we could take
would work. In that case we could take