Closure properties of almost-finiteness classes in recursive function theory

Extract

In this paper we will investigate closure properties of the class of immune sets and of other, more restricted classes of sets of natural numbers under union and similar operations. Our main theorem states that there exists a hyperhyperimmune set A such that A join A is not hyperhyperimmune. We will prove this result in §3. The remaining questions about closure properties are all much easier and will be answered in §2.

We consider the closure properties which are given in the following

Definition. Let bea. class of subsets of N.

(i) is closed under join, if A join B ∈ whenever A ∈ and B ∈ .

(ii) is closed under self-join, if A join A ∈ whenever A ∈ .

(iii) is closed under union, if A ⋃ B ∈ whenever A ∈ and B ∈ .

(iv) is closed under cartesian product, if A × B ∈ whenever A ∈ and B ∈ .

(v) is closed under cartesian self-product, if A × A ∈ whenever A ∈ .

The almost-finiteness classes we consider are the following:

₁ = {X∣X is immune};

₂ = {X∣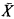 simple};

₃ = {X∣X is hyperimmune};

₄ = {X∣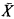 is hypersimple};

₅ = {X∣X is strongly hyperimmune};

₆ = {X∣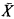 is strongly hypersimple};

₇ = {X∣X is hyperhyperimmune};

₈ = {X∣X is strongly hyperhyperimmune};

₉ = {X∣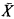 is hyperhypersimple};

₁₀ = {X∣X is dense immune};

₁₁ = {X∣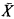 is dense simple}.

The definitions are all contained in Rogers [4, Chapter 12] and/or in Robinson [3]. In addition we could consider the class of -strongly hyperimmune sets and classes defined by lim-properties; see Rogers [4, pp. 243–244]. For other classes, however, such as the class of cohesive sets, the questions become trivial.

Our aim is to establish the table on the next page.