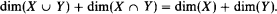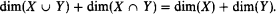Research Article
On the number of generators of cylindric algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 865-873
-
- Article
- Export citation
Some results concerning strongly compact cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 874-880
-
- Article
- Export citation
Nonsplitting subset of
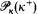 κ(κ+)
κ(κ+)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 881-894
-
- Article
- Export citation
Epistemic set theory is a conservative extension of intuitionistic set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 895-902
-
- Article
- Export citation
The completeness of a predicate-functor logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 903-926
-
- Article
- Export citation
Answer to a problem raised by J. Robinson: The arithmetic of positive or negative integers is definable from successor and divisibility
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 927-935
-
- Article
- Export citation
The ⊲-ordering on normal ultrafilters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 936-952
-
- Article
- Export citation
Polynomial rings and weak second-order logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 953-972
-
- Article
- Export citation
Why some people are excited by Vaught's conjecture
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 973-982
-
- Article
- Export citation
On minimal pairs of enumeration degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 983-1001
-
- Article
- Export citation
A guide to “Coding the universe” by Beller, Jensen, Welch
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1002-1019
-
- Article
- Export citation
A note on nonmultidimensional superstable theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1020-1024
-
- Article
- Export citation
The ideal structure of existentially closed algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1025-1043
-
- Article
- Export citation
The geometry of weakly minimal types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1044-1053
-
- Article
- Export citation
One theorem of Zil′ber's on strongly minimal sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1054-1061
-
- Article
- Export citation
An algorithm to determine, for any prime p, a polynomial-sized Horn sentence which expresses “The cardinality is not p”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1062-1064
-
- Article
- Export citation
Reviews
Andrew Hodges. Alan Turing: the enigma. Burnett Books, London, and Simon and Schuster, New York, 1983, ix + 587 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1065-1067
-
- Article
- Export citation
Robert L. Martin and Peter W. Woodruff. On representing ‘true-in-L' in L. Philosophia (Ramat-Gan), vol. 5 no. 3 (1975), pp. 213–217. (Reprinted in Language in focus: foundation, methods and systems, Essays in memory of Yehoshua Bar-Hillel, edited by Asa Kasher, Boston studies in the philosophy of science, vol. 43, Synthese library, vol. 89, D. Reidel Publishing Company, Dordrecht and Boston 1976, pp. 113–117.) - Saul Kripke. Outline of a theory of truth. The journal of philosophy, vol. 72 (1975), pp. 690–716. - Anil Gupta. Truth and paradox. Journal of philosophical logic, vol. 11 (1982), pp. 1–60. - Hans G. Herzberger. Notes on naive semantics. Journal of philosophical logic, vol. 11 (1982), pp. 61–102.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1068-1071
-
- Article
- Export citation
David Woodruff Smith and Ronald McIntyre. Husserl and intentionattty. A study of mind, meaning, and language. Synthese library, vol. 154. D. Reidel Publishing Company, Dordrecht, Boston, and London, 1982, xxiii + 423 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1071-1073
-
- Article
- Export citation
Ronald Fagin. Probabilities on finite models. The journal of symbolic logic, vol. 41 (1976), pp. 50–58. - Ú. V. Glébskij, D. I. Kogan, M. I. Liongon'kij, and V. A. Talanov. Obém i dolá vypolnimosti formul uzkogo isčisléniá prédikatov. Kibérnétika (Kiev), no. 2 (1969), pp. 17–27. - Yu. V. Glebskii, D. I. Kogan, M. I. Liogon′kii, and V. A. Talanov. Range and degree of realizability of formulas in the restricted predicate calculus. English translation of the preceding. Cybernetics (New York), vol. 5 (for 1969, pub. 1972), pp. 142–154. - James F. Lynch. Almost sure theories. Annals of mathematical logic, vol. 18 (1980), pp. 91–135. - V. L. Murskij. Konéčnaá baziruémost′ toždéstv i drugié svojstva “počti vséh” konéčnyh algébr (A finite basis of identities and other properties of “almost all” finite algebras). Problémy kibérnétiki, vol. 30 (1975), pp. 43–56. - Roy O. Davies. On n-valued Shejfer functions. Zeitschrift für mathematische Logik and Grundlagen der Mathematik, vol. 25 (1979), pp. 293–298.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1073-1076
-
- Article
- Export citation

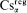 and Cs
and Cs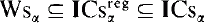 ⊆ CA
⊆ CA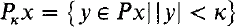 . If also
. If also 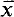 denotes its order type in the natural ordering. The identity function with the domain appropriate to the context is denoted by id. For the notation concerning ultrapowers and elementary embeddings, see [11]. When we talk about forcing, “⊩” will mean “weakly forces” and “
denotes its order type in the natural ordering. The identity function with the domain appropriate to the context is denoted by id. For the notation concerning ultrapowers and elementary embeddings, see [11]. When we talk about forcing, “⊩” will mean “weakly forces” and “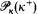
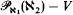 stationary
stationary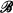 . Second, in a fashion completely analogous to the construction of Boolean-valued models of classical set theory, we define the
. Second, in a fashion completely analogous to the construction of Boolean-valued models of classical set theory, we define the 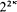 normal ultrafilters, so it is consistent that
normal ultrafilters, so it is consistent that 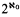
 -generic over
-generic over