No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 12 March 2014
The theory of cylindric algebras (CA's) is the algebraic theory of first order logics. Several ideas about logic are easier to formulate in the frame of CA-theory. Such are e.g. some concepts of abstract model theory (cf. [1] and [10]–[12]) as well as ideas about relationships between several axiomatic theories of different similarity types (cf. [4] and [10]). In contrast with the relationship between Boolean algebras and classical propositional logic, CA's correspond not only to classical first order logic but also to several other ones. Hence CA-theoretic results contain more information than their counterparts in first order logic. For more about this see [1], [3], [5], [9], [10] and [12].
Here we shall use the notation and concepts of the monographs Henkin-Monk-Tarski [7] and [8]. ω denotes the set of natural numbers. CAα denotes the class of all cylindric algebras of dimension α; by “a CAα” we shall understand an element of the class CAα. The class Dcα ⊆ CAα was defined in [7]. Note that Dcα = 0 for α ∈ ω. The classes Wsα,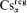 
and Csα were defined in 1.1.1 of [8], p. 4. They are called the classes of all weak cylindric set algebras, regular cylindric set algebras and cylindric set algebras respectively. It is proved in [8] (I.7.13, I.1.9) that 
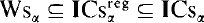⊆ CAα. (These inclusions are proper by 7.3.7, 1.4.3 and 1.5.3 of [8].)
It was proved in 2.3.22 and 2.3.23 of [7] that every simple, finitely generated Dcα is generated by a single element. This is the algebraic counterpart of a property of first order logics (cf. 2.3.23 of [7]). The question arose: for which simple CAα's does “finitely generated” imply “generated by a single element” (see p. 291 and Problem 2.3 in [7]). In terms of abstract model theory this amounts to asking the question: For which logics does the property described in 2.3.23 of [7] hold? This property is roughly the following. In any maximal theory any finite set of concepts is definable in terms of a single concept. The connection with CA-theory is that maximal theories correspond to simple CA's (the elements of which are the concepts of the original logic) and definability corresponds to generation.