Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T03:09:22.747Z Has data issue: false hasContentIssue false
  • English
  • Français

Epistemic set theory is a conservative extension of intuitionistic set theory

Published online by Cambridge University Press:  12 March 2014

R. C. Flagg
R. C. Flagg*
Affiliation:
Department of Mathematics, State University of New Yorkat Buffalo, Buffalo, New York 14214
Get access Rights & Permissions [Opens in a new window]

Extract

In [6] Gödel observed that intuitionistic propositional logic can be interpreted in Lewis's modal logic (S4). The idea behind this interpretation is to regard the modal operator □ as expressing the epistemic notion of “informal provability”. With the work of Shapiro [12], Myhill [10], Goodman [7], [8], and Ščedrov [11] this simple idea has developed into a successful program of integrating classical and intuitionistic mathematics.

There is one question quite central to the above program that has remained open. Namely:

Does Ščedrov's extension of the Gödel translation to set theory provide a faithful interpretation of intuitionistic set theory into epistemic set theory?

In the present paper we give an affirmative answer to this question.

The main ingredient in our proof is the construction of an interpretation of epistemic set theory into intuitionistic set theory which is inverse to the Gödel translation. This is accomplished in two steps. First we observe that Funayama's theorem is constructively provable and apply it to the power set of 1. This provides an embedding of the set of propositions into a complete topological Boolean algebra 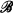. Second, in a fashion completely analogous to the construction of Boolean-valued models of classical set theory, we define the 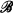-valued universe 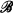V(). V(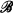) gives a model of epistemic set theory and, since we use a constructive metatheory, this provides an interpretation of epistemic set theory into intuitionistic set theory.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 4 , December 1985 , pp. 895 - 902
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bell, J. L., Boolean-valued models and independence proofs in set theory, Clarendon Press, Oxford, 1977.Google Scholar
[2]Flagg, R. C., Church's thesis is consistent with epistemic arithmetic, [13], pp. 121–172.CrossRefGoogle Scholar
[3]Flagg, R. C., Integrating classical and intuitionistic type theory, Annals of Pure and Applied Logic (to appear).Google Scholar
[4]Fourman, M. P. and Scott, D. S., Sheaves and logic, Applications of sheaves (Fourman, M., Mulvey, C. and Scott, D., editors), Lectures Notes in Mathematics, vol. 753, Springer-Verlag, Berlin, 1979, pp. 113–170.CrossRefGoogle Scholar
[5]Friedman, H., The consistency of classical set theory relative to a set theory with intuitionistic logic, this Journal, vol. 38 (1973), pp. 315–319.Google Scholar
[6]Gödel, K., Eine Interpretation des intuitionistischen Aussagenkalküls, Ergebnisse eines Mathematischen Kolloquiums, vol. 4 (1932), pp. 39–40.Google Scholar
[7]Goodman, N. D., A genuinely intensional set theory, [13], pp. 63–80.CrossRefGoogle Scholar
[8]Goodman, N. D., Epistemic arithmetic is a conservative extension of intuitionistic arithmetic, this Journal, vol. 49 (1984), pp. 192–203.Google Scholar
[9]Grayson, R. J., Heyting-valued models for intuitionistic set theory, Applications of sheaves (Fourman, M., Mulvey, C. and Scott, D., editors), Lecture Notes in Mathematics, vol. 753, Springer-Verlag, Berlin, 1979, pp. 402–414.CrossRefGoogle Scholar
[10]Myhill, J., Intensional set theory, [13], pp. 47–62.CrossRefGoogle Scholar
[11]Ščedrov, A., Extending Gödel's modal interpretation to type theory and set theory, [13], pp. 81–120.CrossRefGoogle Scholar
[12]Shapiro, S., Epistemic and intuitionistic arithmetic, [13], pp. 11–46.CrossRefGoogle Scholar
[13]Shapiro, S. (editor), Intensional mathematics, North-Holland, Amsterdam, 1985.Google Scholar