Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T01:29:14.836Z Has data issue: false hasContentIssue false
  • English
  • Français

A guide to “Coding the universe” by Beller, Jensen, Welch

Published online by Cambridge University Press:  12 March 2014

Sy D. Friedman
Sy D. Friedman*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139
Get access Rights & Permissions [Opens in a new window]

Extract

In the wake of Silver's breakthrough on the Singular Cardinals Problem (Silver [74]) followed one of the landmark results in set theory, Jensen's Covering Lemma (Devlin-Jensen [74]): If 0# does not exist then for every uncountable x ⊆ ORD there exists a constructible Y ⊇ X, card(Y) = card(X). Thus it is fair to say that in the absence of large cardinals, V is “close to L”.

It is natural to ask, as did Solovay, if we can fairly interpret the phrase “close to L” to mean “generic over L”. For example, if V = L[a], a ⊆ ω and if 0# does not exist then is V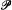-generic over L for some partial ordering 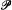∈ L? Notice that an affirmative answer implies that in the absence of 0#, no real can “code” a proper class of information.

Jensen's Coding Theorem provides a negative answer to Solovay's question, in a striking way: Any class can be “coded” by a real without introducing 0#. More precisely, if A ⊆ ORD then there is a forcing 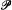definable over 〈L[A], A〉 such that 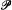⊩ V = L[a], a ⊆ ω, A is definable from a. Moreover if 0# ∉ L[A] then 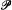⊩ 0# does not exist. Now as any M ⊨ ZFC can be generically extended to a model of the form L[A] (without introducing 0#) we obtain: For any 〈M, A〉 ⊨ ZFC (that is, M ⊨ ZFC and M obeys Replacement for formulas mentioning A as a predicate) there is an 〈M, A〉-definable forcing 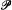such that 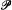⊩ V = L[a], a ⊆ ω, 〈M, A〉 is definable from a. Moreover if 0# ∉ M then 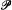⊩ 0# does not exist.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 4 , December 1985 , pp. 1002 - 1019
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Beller, A., Jensen, R. and Welch, P. [82], Coding the universe, London Mathematical Society Lecture Note Series, vol. 47, Cambridge University Press, Cambridge.Google Scholar
David, R. [82], Some applications of Jensen's coding theorem, Annals of Mathematical Logic, vol. 22, pp. 177–196.CrossRefGoogle Scholar
David, R. [83], A functorial -singleton, Advances in Mathematics (to appear).Google Scholar
Devlin, K. and Jensen, R. B. [74], Marginalia to a theorem of Silver, ⊨ ISILC logic conference (Kiel, 1974), Lecture Notes in Mathematics, vol. 499, Springer-Verlag, Berlin, 1975, pp. 115–142.CrossRefGoogle Scholar
Easton, W. [70], Powers of regular cardinals, Annals of Mathematical Logic, vol. 1, pp. 139–178.CrossRefGoogle Scholar
Jensen, R. B. and Solovay, R. [68], Some applications of almost disjoint sets, Mathematical logic and the foundations of set theory (Bar-Hillel, Y., editor), North-Holland, Amsterdam, 1970, pp. 84–104.Google Scholar
Silver, J. [74], On the singular cardinals problem, Proceedings of the International Congress of Mathematicians (Vancouver, 1974), vol. 1, Canadian Mathematical Congress, Montréal, 1975, pp. 265–268.Google Scholar