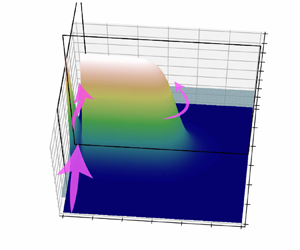
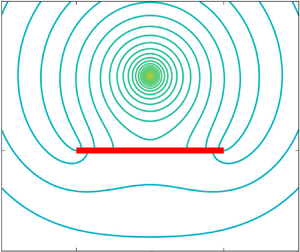
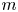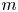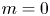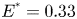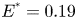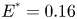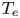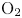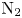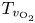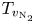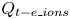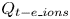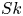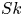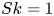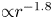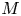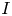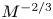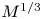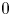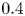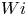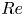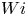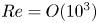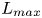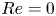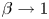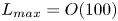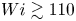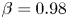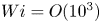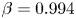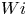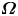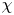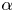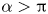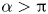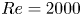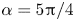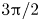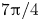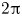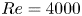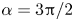Moore, M., Vella, D. & Oliver, J. 2022 The nascent coffee ring with arbitrary droplet contact set: an asymptotic analysis. J. Fluid Mech. 940, A38. doi:10.1017/jfm.2022.251.
Editorial
(Dawning of a) New era for JFM
-
- Published online by Cambridge University Press:
- 19 April 2022, E1
-
- Article
-
- You have access
- HTML
- Export citation
JFM Rapids
A robust physics-based method to filter coherent wavepackets from high-speed schlieren images
-
- Published online by Cambridge University Press:
- 05 April 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimating the non-dimensional energy of vortex rings by modelling their roll-up
-
- Published online by Cambridge University Press:
- 20 April 2022, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Focus on Fluids
Bounded dissipation predicts finite asymptotic state of near-wall turbulence
-
- Published online by Cambridge University Press:
- 05 April 2022, F1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Batchelor Prize Lecture: Measurements in wall-bounded turbulence
-
- Published online by Cambridge University Press:
- 05 April 2022, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isolating effects of Darrieus–Landau instability on the morphology and propagation of turbulent premixed flames
-
- Published online by Cambridge University Press:
- 05 April 2022, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theoretical and numerical study of the binary scaling law for electron distribution in thermochemical non-equilibrium flows under extremely high Mach number
-
- Published online by Cambridge University Press:
- 05 April 2022, A3
-
- Article
- Export citation
Scale-dependent particle clustering in transitional wake flow
-
- Published online by Cambridge University Press:
- 05 April 2022, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Comprehensive analysis of spherical bubble oscillations and shock wave emission in laser-induced cavitation
-
- Published online by Cambridge University Press:
- 12 April 2022, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Skimming impact of a thin heavy body on a shallow liquid layer
-
- Published online by Cambridge University Press:
- 06 April 2022, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Comparative study on single-incident and dual-incident shock wave/turbulent boundary layer interactions with identical total deflection angle
-
- Published online by Cambridge University Press:
- 05 April 2022, A7
-
- Article
- Export citation
Hydraulic control of flow in a multi-passage system connecting two basins
-
- Published online by Cambridge University Press:
- 05 April 2022, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A playground for compressible natural convection with a nearly uniform density
-
- Published online by Cambridge University Press:
- 05 April 2022, A9
-
- Article
- Export citation
Nanoscale sheared droplet: volume-of-fluid, phase-field and no-slip molecular dynamics
-
- Published online by Cambridge University Press:
- 06 April 2022, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weakly nonlinear analysis of the viscoelastic instability in channel flow for finite and vanishing Reynolds numbers
-
- Published online by Cambridge University Press:
- 08 April 2022, A11
-
- Article
- Export citation
Diffusiophoretic propulsion of an isotropic active colloidal particle near a finite-sized disk embedded in a planar fluid–fluid interface
-
- Published online by Cambridge University Press:
- 06 April 2022, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unsteady chiral swimmer and its response to a chemical gradient
-
- Published online by Cambridge University Press:
- 06 April 2022, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling silo clogging with non-local granular rheology
-
- Published online by Cambridge University Press:
- 06 April 2022, A14
-
- Article
- Export citation
Interfacial electrohydrodynamic solitary waves under horizontal electric fields
-
- Published online by Cambridge University Press:
- 06 April 2022, A15
-
- Article
- Export citation
Turbulent flows along a streamwise external corner
-
- Published online by Cambridge University Press:
- 06 April 2022, A16
-
- Article
- Export citation