Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T03:14:44.743Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent flows along a streamwise external corner

Published online by Cambridge University Press:  06 April 2022

Nikolay Nikitin Open the ORCID record for Nikolay Nikitin [Opens in a new window]  and
Boris Krasnopolsky
Nikolay Nikitin*
Affiliation:
Institute of Mechanics, Lomonosov Moscow State University, 1 Michurinsky prospect, 119899 Moscow, Russia
Boris Krasnopolsky
Affiliation:
Institute of Mechanics, Lomonosov Moscow State University, 1 Michurinsky prospect, 119899 Moscow, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

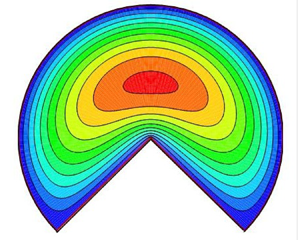
A numerical investigation of turbulent flows in straight pipes with a cross-section in the form of a circular sector at different values of the apex angle ${\alpha }$ is carried out. Main attention is paid to the cases ${\alpha }>{\rm \pi}$ when the cross-section boundary contains a convex external corner. An analytical solution to the problem of laminar flow in the geometry under consideration is given. The law of resistance is determined, and velocity distributions over the pipe cross-section are obtained. The singularity of wall shear stress $\tau _w\sim r^{{\rm \pi} /{\alpha }-1}$ at ${\alpha }>{\rm \pi}$ is shown which persists in turbulent flows as well. Turbulent flows are simulated at $Re=2000$ and four apex-angle values ${\alpha }=5{\rm \pi} /4$, $3{\rm \pi} /2$, $7{\rm \pi} /4$ and $2{\rm \pi}$, as well as at a larger $Re=4000$ and ${\alpha }=3{\rm \pi} /2$. The characteristic features of the mean-velocity distributions are outlined, and their relationship with secondary flows is shown. The velocity of the secondary flow in the vicinity of the external corner reaches the value $6.3\,\%$ of the bulk flow velocity at the maximum ${\alpha }=2{\rm \pi}$. A characteristic feature of the considered flows is the presence of intense transverse velocity fluctuations in the region above the apex corner. It is hypothesized that the cause of these fluctuations may be the linear instability of the mean flow field. The studies of linear stability confirm this hypothesis. Considerable attention is paid to the study of secondary flows in the vicinity of the external corner. In general, the formation of these flows fits into the scheme proposed earlier (Nikitin, J. Fluid Mech., vol. 917, 2021, A24; Nikitin et al., Fluid Dyn., vol. 56, issue 4, 2021, pp. 513–538), according to which the main mechanism is the centrifugal force arising from the fluctuating flow over the corner in the transverse plane. It is shown that the shape of secondary flows is reproduced to a certain extent by the vortical part of the Reynolds-stress force field. The latter may be found from the Helmholtz decomposition. The features of the mean pressure distribution associated with the secondary flow and with the presence of a region of concentrated fluctuations above the external corner are explained.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Pipe flow Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 940 , 10 June 2022 , A16
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bhaganagar, K., Kim, J. & Coleman, G. 2004 Effect of roughness on wall-bounded turbulence. Flow Turbul. Combust. 72 (2–4), 463–492.CrossRefGoogle Scholar
Brundrett, E. & Baines, W.D. 1964 The production and diffusion of vorticity in duct flow. J. Fluid Mech. 19 (3), 375–394.CrossRefGoogle Scholar
Castro, I.P., Kim, J.W., Stroh, A. & Lim, H.C. 2021 Channel flow with large longitudinal ribs. J. Fluid Mech. 915, A92.CrossRefGoogle Scholar
Chan, L., Macdonald, M., Chung, D., Hutchins, N. & Ooi, A. 2018 Secondary motion in turbulent pipe flow with three-dimensional roughness. J. Fluid Mech. 854, 5–33.CrossRefGoogle Scholar
Einstein, H.A. & Li, H. 1958 Secondary currents in straight channels. Trans. Am. Geophys. Union 39 (6), 1085–1088.CrossRefGoogle Scholar
Elingsen, S.Å., Akselsen, A.H. & Chan, L. 2021 Designing vortices in pipe flow with topography-driven Langmuir circulation. J. Fluid Mech. 926, A9.CrossRefGoogle Scholar
Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.CrossRefGoogle Scholar
Goldstein, D.B. & Tuan, T.-C. 1998 Secondary flow induced by riblets. J. Fluid Mech. 363, 115–151.CrossRefGoogle Scholar
Huser, A. & Biringen, S. 1993 Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 257, 65–95.CrossRefGoogle Scholar
Hwang, H. & Lee, J. 2018 Secondary flows in turbulent boundary layers over longitudinal surface roughness. Phys. Rev. Fluids 3 (1), 014608.CrossRefGoogle Scholar
Kornilov, V.I. 2017 Three-dimensional turbulent near-wall flows in streamwise corners: current state and questions. Prog. Aerosp. Sci. 94, 46–81.CrossRefGoogle Scholar
Moinuddin, K.A.M., Joubert, P.N. & Chong, M.S. 2004 Experimental investigation of turbulence-driven secondary motion over a streamwise external corner. J. Fluid Mech. 511, 1–23.CrossRefGoogle Scholar
Nikitin, N. 2006 a Third-order-accurate semi-implicit Runge–Kutta scheme for incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 51 (2), 221–233.CrossRefGoogle Scholar
Nikitin, N. 2006 b Finite-difference method for incompressible Navier–Stokes equations in arbitrary orthogonal curvilinear coordinates. J. Comput. Phys. 217, 759–781.CrossRefGoogle Scholar
Nikitin, N. 2021 Turbulent secondary flows in channels with no-slip and shear-free boundaries. J. Fluid Mech. 917, A24.CrossRefGoogle Scholar
Nikitin, N. & Yakhot, A. 2005 Direct numerical simulation of turbulent flow in elliptical ducts. J. Fluid Mech. 532, 141–164.CrossRefGoogle Scholar
Nikitin, N.V., Popelenskaya, N.V. & Stroh, A. 2021 Prandtl's secondary flows of the second kind. Problems of description, prediction, and simulation. Fluid Dyn. 56 (4), 513–538.CrossRefGoogle Scholar
Panchapakesan, N.R. & Joubert, P.N. 1998 Turbulent boundary layer development along a streamwise edge (Chine)-mean flow. In 13th Australasian Fluid Mechanics Conference, Monash, 1998 (ed. M.C. Thompson & K. Hourigan), pp. 373–376. Monash University Publishing.Google Scholar
Panchapakesan, N.R. & Joubert, P.N. 1999 Turbulence measurements in the boundary layer over a streamwise edge (Chine). In Turbulence and Shear flow Phenomena, Santa Barbara, 1999, (S. Banerjee & J.K. Eaton). Begell House.Google Scholar
Pinelli, A., Uhlmann, M., Sekimoto, A. & Kawahara, G. 2010 Reynolds number dependence of mean flow structure in square duct turbulence. J. Fluid Mech. 644, 107–122.CrossRefGoogle Scholar
Pirozzoli, S., Modesti, D., Orlandi, P. & Grasso, F. 2018 Turbulence and secondary motions in square duct flow. J. Fluid Mech. 840, 631–655.CrossRefGoogle Scholar
Prandtl, L. 1931 Einführung in die Grundbegriffe der Strömungslehre. Akademische Verlagsgesellschaft.Google Scholar
Speziale, C.G. 1982 On turbulent secondary flows in pipes of noncircular cross-section. Intl J. Engng Sci. 20 (7), 863–872.CrossRefGoogle Scholar
Stroh, A., Schäfer, K., Forooghi, P. & Frohnapfel, B. 2020 Secondary flow and heat transfer in turbulent flow over streamwise ridges. Intl J. Heat Fluid Flow 81, 108518.CrossRefGoogle Scholar
Uhlmann, M., Pinelli, A., Kawahara, G. & Sekimoto, A. 2007 Marginally turbulent flow in a square duct. J. Fluid Mech. 588, 153–162.CrossRefGoogle Scholar
Vanderwel, C. & Ganapathisubramani, B. 2015 Effects of spanwise spacing on large-scale secondary flows in rough-wall turbulent boundary layers. J. Fluid Mech. 774, 1–12.CrossRefGoogle Scholar
Vanderwel, C., Stroh, A., Kriegseis, J., Frohnapfel, B. & Ganapathisubramani, B. 2019 The instantaneous structure of secondary flows in turbulent boundary layers. J. Fluid Mech. 862, 845–870.CrossRefGoogle Scholar
White, F.M. 2006 Viscous Fluid Flow, 3rd edn, International edn. McGraw-Hill.Google Scholar
Xu, H. & Pollard, A. 2001 Large eddy simulation of turbulent flow in a square annular duct. Phys. Fluids 13 (11), 3321–3337.CrossRefGoogle Scholar
Xu, H. 2009 Direct numerical simulation of turbulence in a square annular duct. J. Fluid Mech. 621, 23–57.CrossRefGoogle Scholar