While it has long been recognized that Lagrangian drift at the ocean surface plays a critical role in the kinematics and dynamics of upper ocean processes, only recently has the contribution of wave breaking to this drift begun to be investigated through direct numerical simulations (Deike et al., J. Fluid Mech., vol. 829, 2017, pp. 364–391; Pizzo et al., J. Phys. Oceanogr., vol. 49(4), 2019, pp. 983–992). In this work, laboratory measurements of the surface Lagrangian transport due to focusing deep-water non-breaking and breaking waves are presented. It is found that wave breaking greatly enhances mass transport, compared to non-breaking focusing wave packets. These results are in agreement with the direct numerical simulations of Deike et al. (J. Fluid Mech., vol. 829, 2017, pp. 364–391), and the increased transport due to breaking agrees with their scaling argument. In particular, the transport at the surface scales with $S$, the linear prediction of the maximum slope at focusing, while the surface transport due to non-breaking waves scales with $S^{2}$, in agreement with the classical Stokes prediction.

We show experimentally that the mechanisms of energy transport in turbulent flows of superfluid $^{4}\text{He}$ are strikingly different from those occurring in turbulent flows of viscous fluids. We argue that the result can be related to the role played by quantized vortices in this unique type of turbulence. The flow-induced motions of relatively small particles suspended in the liquid reveal that, for scales of the order of the mean distance between the vortices, the particles do not tend on average to decelerate faster than they accelerate, whereas, at larger scales, a classical-like asymmetry is recovered. It follows that, in the range of investigated parameters, flight-crash events are less apparent than in classical turbulence. We specifically link the outcome to the time symmetry of quantized vortex reconnections observed at scales comparable to the typical particle size.

In a recent paper (J. Fluid Mech., vol. 861, 2019, pp. 328–348), Benilov derived equations governing a laminar liquid sheet (a curtain) that emanates from a slot whose centreline is inclined to the vertical. The equations are valid for slender sheets whose characteristic length scale in the direction of flow is much larger than its cross-sectional thickness. For a liquid that leaves a slot with average speed, $u_{0}$, volumetric flow rate per unit width, $q$, surface tension, $\unicode[STIX]{x1D70E}$, and density, $\unicode[STIX]{x1D70C}$, Benilov obtains parametric equations that predict steady-state curtain shapes that bend upwards against gravity provided $\unicode[STIX]{x1D70C}qu_{0}/2\unicode[STIX]{x1D70E}<1$. Benilov’s parametric equations are shown to be identical to those derived by Finnicum, Weinstein, and Ruschak (J. Fluid Mech., vol. 255, 1993, pp. 647–665). In the latter form, it is straightforward to deduce an alternative solution of Benilov’s equations where a curtain falls vertically regardless of the slot’s orientation. This solution is consistent with prior experimental and theoretical results that show that a liquid curtain can emerge from a slot at an angle different from that of the slot centreline.

We have studied the motion of drops on inclined liquid-impregnated surfaces (LISs) subject to vertical vibrations. The liquid drops comprise distilled water and different aqueous solutions of glycerol of increasing viscosity. The use of weak pinning LISs strongly affects the dynamical phase diagram. First of all, there is no trace of the dominant static region at low oscillating amplitudes reported for oscillating solid surfaces characterized by contact angle hysteresis. On the contrary, at sufficiently low oscillating amplitudes, the drops always move downwards with a velocity that depends only on the drop viscosity. Further increasing the oscillating amplitude may drive the drop upwards against gravity, as reported for dry surfaces. The use of more viscous drops widens this climbing region. Arguably, the main novelty of this work concerns the observation of two distinct descending regimes where the downhill speed differs by a factor of five or more. Fast-rate videos show that the evolution of the drop profile is diverse in the two regimes, likely because the vertical oscillations reduce the effect of the oil meniscus surrounding the drop at high accelerations.

A primary objective in turbulent thermal convection research is to understand and control the heat transport scaling behaviour. Previous studies have shown that the heat transport can be tuned by manipulating the boundary layer topographies with monoscale roughness elements. Now, Zhu et al. (J. Fluid Mech., vol. 869, 2019, R4) have demonstrated that with multiscale wall roughness, the heat transport law with an exponent of $1/2$ can be achieved for an extended range of the Rayleigh number, providing a new way to manipulate heat transport by tuning boundary topographies in turbulent flows.

In an earlier paper (Wan et al., J. Fluid Mech., vol. 697, 2012, pp. 296–315), the authors showed that a similarity solution for anisotropic incompressible three-dimensional magnetohydrodynamic (MHD) turbulence, in the presence of a uniform mean magnetic field $\boldsymbol{B}_{0}$, exists if the ratio of parallel to perpendicular (with respect to $\boldsymbol{B}_{0}$) similarity length scales remains constant in time. This conjecture appears to be a rather stringent constraint on the dynamics of decay of the energy-containing eddies in MHD turbulence. However, we show here, using direct numerical simulations, that this hypothesis is indeed satisfied in incompressible MHD turbulence. After an initial transient period, the ratio of parallel to perpendicular length scales fluctuates around a steady value during the decay of the eddies. We show further that a Taylor–Kármán-like similarity decay holds for MHD turbulence in the presence of a mean magnetic field. The effect of different parameters, including Reynolds number, mean field strength, and cross-helicity, on the nature of similarity decay is discussed.

The rotational behaviour of non-spherical particles in turbulent channel flow is studied by Lagrangian tracking of spheroidal point particles in a directly simulated flow. The focus is on the complex rotation modes of the spheroidal particles, in which the back reaction on the flow field is ignored. This study is a sequel to the letter by Zhao et al. (Phys. Rev. Lett., vol. 115, 2015, 244501), in which only selected results in the near-wall buffer region and the almost-isotropic channel centre were presented. Now, particle dynamics all across the channel is explored to provide a complete picture of the orientational and rotational behaviour with consideration of the effects of particle aspect ratio ranging from 0.1 to 10 and particle Stokes number from 0 (inertialess) to 30. The rotational dynamics in the innermost part of the logarithmic wall layer is particularly complex and affected not only by modest mean shear, but also by particle inertia and turbulent vorticity. While inertial disks exhibit modest preferential orientation in either the wall-normal or cross-stream direction, inertial rods show neither preferential tumbling nor spinning. Examination of the co-variances between particle orientation, particle rotation and fluid rotation vectors explains the qualitatively different ‘wall mode’ rotation and ‘centre mode’ rotation. Inertialess spheroids transition between the two modes within a narrow zone ($15<z^{+}<35$) in the buffer region. If the spheroids have inertia, the transition zone between the two modes shifts to the inner part of the logarithmic layer, i.e. $z^{+}\geqslant 40$. We ascribe the transition of inertialess spheroids from the ‘wall mode’ to the ‘centre mode’ rotation to the changeover between the time scales associated with mean shear and small-scale turbulence. Inertial spheroids, however, transition between the two rotational modes when the Kolmogorov time scale becomes comparable to the time scale for particle rotation, i.e. the effective Stokes number is of order unity. The aforementioned findings reveal, in addition to the effects of particle shape and alignment, the importance of the characteristic local time scale of fluid flow for the rotation of both tracer and inertial spheroids in turbulent channel flows.

This work is concerned with waves propagating on water of finite depth with a constant-vorticity current under a deformable flexible sheet. The pressure exerted by the sheet is modelled by using the Cosserat thin shell theory. By means of multi-scale analysis, small amplitude nonlinear modulation equations in several regimes are considered, including the nonlinear Schrödinger equation (NLS) which is used to predict the existence of small-amplitude wavepacket solitary waves in the full Euler equations and to study the modulational instability of quasi-monochromatic wavetrains. Guided by these weakly nonlinear results, fully nonlinear steady and time-dependent computations are performed by employing a conformal mapping technique. Bifurcation mechanisms and typical profiles of solitary waves for different underlying shear currents are presented in detail. It is shown that even when small-amplitude solitary waves are not predicted by the weakly nonlinear theory, we can numerically find large-amplitude solitary waves in the fully nonlinear equations. Time-dependent simulations are carried out to confirm the modulational stability results and illustrate possible outcomes of the nonlinear evolution in unstable cases.

Laminar-to-turbulent transition in a zero-pressure-gradient boundary layer at Mach 4.5 is studied using direct numerical simulations. For a given level of total disturbance energy, the inflow spectrum was designed to correspond to the nonlinearly most dangerous condition that leads to the earliest possible transition Reynolds number. The synthesis of the inlet disturbance is formulated as a constrained optimization, where the control vector is comprised of the amplitudes and relative phases of the inlet modes; the constraints are the prescribed total energy and that the flow evolution satisfies the full nonlinear compressible Navier–Stokes equations; the cost function is defined in terms of the mean skin-friction coefficient and, once maximized, ensures the earliest possible transition location. An ensemble-variational (EnVar) technique is developed to solve the optimization problem. Starting from an initial guess, here a broadband disturbance, EnVar updates the estimate of the control vector at the end of each iteration using the gradient of the cost function, which is evaluated from the outcomes of an ensemble of possible solutions. Two inflow conditions are computed, each corresponding to a different level of energy, and their spectra are contrasted: the lower-energy case includes two normal acoustic waves and one oblique vorticity perturbation, whereas the higher-energy condition consists of oblique acoustic and vorticity waves. The focus is placed on the former case because it cannot be categorized as any of the classical breakdown scenarios (fundamental, subharmonic or oblique), while the higher-energy condition undergoes a second-mode oblique transition. At the lower energy level, the instability wave that initiates the rapid breakdown to turbulence is not present at the inlet plane. Instead, it appears at a downstream location after a series of nonlinear interactions that spur the fastest onset of turbulence. The results from the nonlinearly most potent inflow condition are also compared to other inlet disturbances that are selected solely based on linear theory, and which all yield relatively delayed transition onset.

The response of a floating elastic plate to the motion of a moving load is studied using a fully dispersive weakly nonlinear system of equations. The system allows for an accurate description of waves across the whole spectrum of wavelengths and also incorporates nonlinearity, forcing and damping. The flexural–gravity waves described by the system are time-dependent responses to a forcing with a described weight distribution, moving at a time-dependent velocity. The model is versatile enough to allow the study of a wide range of situations including the motion of a combination of point loads and loads of arbitrary shape. Numerical solutions of the system are compared to data from a number of field campaigns on ice-covered lakes, and good agreement between the deflectometer records and the numerical simulations is observed in most cases. Consideration is also given to waves generated by a decelerating load, and it is shown that a decelerating load may trigger a wave response with a far greater amplitude than a load moving at constant celerity.

A discrete adjoint-based method is employed to control multi-mode Rayleigh–Taylor (RT) instabilities via strategic manipulation of the initial interfacial perturbations. We seek to find to what extent mixing and growth can be enhanced at late stages of the instability and which modes are targeted to achieve this. Three objective functions are defined to quantify RT mixing and growth: (i) variance of mole fraction, (ii) a kinetic energy norm based on the vertical velocity and (iii) variations of mole fraction with respect to the unperturbed initial state. The sensitivity of these objective functions to individual amplitudes of the initial perturbations are studied at various stages of the RT instability. The most sensitive wavenumber during the early stages of the instability closely matches the most unstable wavenumber predicted by linear stability theory. It is also shown that randomly changing the initial perturbations has little effect at early stages, but results in large variations in both RT growth and its sensitivity at later times. The sensitivity obtained from the adjoint solution is employed in gradient-based optimization to both suppress and enhance the objective functions. The adjoint-based optimization framework was capable of completely suppressing mixing by shifting all of the interfacial perturbation energy to the highest modes such that diffusion dominates. The optimal initial perturbations for enhancing the objective functions were found to have a broadband spectrum resulting in non-trivial coupling between modes and depends on the particular objective function being optimized. The objective functions were increased by as much as a factor of nine in the self-similar late-stage growth regime compared to an interface with a uniform distribution of modes, corresponding to a 32% increase in the bubble growth parameter and 54% increase in the mixing width. It was also found that the interfacial perturbations optimized at early stages of the instability are unable to predict enhanced mixing at later times, and thus optimizing late-time multi-mode RT instabilities requires late-time sensitivity information. Finally, it was found that the optimized distribution of interfacial perturbations obtained from two-dimensional simulations was capable of enhancing the objective functions in three-dimensional flows. As much as 51% and 99% enhancement in the bubble growth parameter and mixing width, respectively, was achieved, even greater than what was reached in two dimensions.

A study of variable-density homogeneous stationary isotropic turbulence based on the sparse direct-interaction perturbation (SDIP) and supporting direct numerical simulations (DNS) is presented. The non-solenoidal flow considered here is an example of turbulent mixing of gases with different densities. The spectral statistics of this type of flow are substantially more difficult to understand theoretically than those of the similar solenoidal flows. In the approach described here, the nonlinearly coupled velocity and scalar (which determine the density of the fluid) equations are expanded in terms of a normalised density ratio parameter. A new set of coupled integro-differential SDIP equations are derived and then solved numerically for the first-order correction to the incompressible equations in the variable-density expansion parameter. By adopting a regular expansion approach, one obtains leading-order corrections that are universal and therefore interesting in their own right. The predictions are then compared with DNS of forced variable-density flow with different density contrasts. It is found that the velocity spectrum owing to variable density is indistinguishable from that of constant-density turbulence, as it is supported by a wealth of indirect experimental evidence, but the scalar spectra show significant deviations, and even loss of monotonicity, as a function of the type and strength of the large-scale source of the mixing. Furthermore, the analysis helps clarify what may be the proper approach to interpret the power spectrum of variable-density turbulence.

The unsteady lift response of an airfoil in a sinusoidal gust has in the past been modelled by two different transfer functions: the first-order Sears function and the second-order Atassi function. Previous studies have shown that the Sears function holds in experiments, but recently Cordes et al. (J. Fluid Mech., vol. 811, 2017) reported experimental data that corresponded to the Atassi function rather than the Sears function. In order to clarify the observed discrepancy, the specific differences between these models are isolated analytically. To this end, data and analysis are confined to unloaded airfoils. These differences are related to physical gust parameters, and gusts with these parameters are then produced in wind-tunnel experiments using an active-grid gust generator. Measurements of the unsteady gust loads on an airfoil in the wind tunnel at Reynolds numbers ($Re_{c}$) of $2.0\times 10^{5}$ and $2.6\times 10^{5}$ and reduced frequencies between $0.09$ and $0.42$ confirm that the Sears and Atassi functions differ only in convention: the additional gust component of the Atassi problem can be scaled so that the Atassi function collapses onto the Sears function. These experiments, complemented by numerical simulations of the set-up, validate both models across a range of gust parameters. Finally, the influence of boundary-layer turbulence and the turbulent wake of the gust generator on experimental convergence with model predictions is investigated. These results serve to clarify the conditions under which the Sears and Atassi functions can be applied, and demonstrate that the Sears function can effectively model unsteady forces even when significant fluctuations in the streamwise velocity are present.

Oblique detonation waves (ODWs) have been studied widely to facilitate their employment in hypersonic propulsion, but the effects of continuous unsteady inflow have never been addressed so far. Thus, the present study investigates wedge-induced oblique detonations in unsteady flow via numerical simulations based on the reactive Euler equations with a two-step induction–reaction kinetic model. As a first step, the chemical and flow parameters are chosen for the simplest structure such that the ODW initiation occurs under a smooth transition with a curved shock. After a steady ODW with smooth initiation transition is established, the inflow is then subject to a continuous sinusoidal density/temperature disturbance. Cases with single-pulse inflow variation are also simulated to clarify whether the observed phenomena are derived solely from the continuous disturbance. Two aspects are analysed to investigate the features of ODWs in unsteady flow, namely, the formation of triple points on the surface, and the movement of the reactive front position. On the formation of triple points, the continuous disturbance generates at most one pair of triple points, less than or equal to the number of triple points in single-pulse cases. This indicates that the effects of continuous disturbance weaken the ability to generate the triple points, although there appear more triple points convected downstream on the surface at any given instant. On the movement of the reactive front, oscillatory behaviours are induced in either single-pulse or continuous disturbance cases. However, more complicated dynamic displacements and noticeable effects of unsteadiness are observed in the cases of continuous disturbance, and are found to be sensitive to the disturbance wavenumber, $N$. Increasing $N$ results in three regimes with distinct behaviours, which are quasi-steady, overshooting oscillation and unstable ODW. For the quasi-steady case with low $N$, the reactive front oscillates coherently with the inflow disturbance with slightly higher amplitude around the initiation region. The overshooting oscillation generates the most significant variation of downstream surface in the case of modest $N$, reflecting a resonance-like behaviour of unsteady ODW. In the case of high $N$, the disturbed ODW surface readjusts itself with local unstable features. It becomes more robust and the reactive front of the final unstable ODW structure is less susceptible to flow disturbance.

The influence of the nozzle-exit boundary-layer profile on high-subsonic jets is investigated by performing compressible large-eddy simulations (LES) for three isothermal jets at a Mach number of 0.9 and a diameter-based Reynolds number of $5\times 10^{4}$, and by conducting linear stability analyses from the mean-flow fields. At the exit section of a pipe nozzle, the jets exhibit boundary layers of momentum thickness of approximately 2.8 % of the nozzle radius and a peak value of turbulence intensity of 6 %. The boundary-layer shape factors, however, vary and are equal to 2.29, 1.96 and 1.71. The LES flow and sound fields differ significantly between the first jet with a laminar mean exit velocity profile and the two others with transitional profiles. They are close to each other in these two cases, suggesting that similar results would also be obtained for a jet with a turbulent profile. For the two jets with non-laminar profiles, the instability waves in the near-nozzle region emerge at higher frequencies, the mixing layers spread more slowly and contain weaker low-frequency velocity fluctuations and the noise levels in the acoustic field are lower by 2–3 dB compared to the laminar case. These trends can be explained by the linear stability analyses. For the laminar boundary-layer profile, the initial shear-layer instability waves are most strongly amplified at a momentum-thickness-based Strouhal number $St_{\unicode[STIX]{x1D703}}=0.018$, which is very similar to the value obtained downstream in the mixing-layer velocity profiles. For the transitional profiles, on the contrary, they predominantly grow at higher Strouhal numbers, around $St_{\unicode[STIX]{x1D703}}=0.026$ and 0.032, respectively. As a consequence, the instability waves rapidly vanish during the boundary-layer/shear-layer transition in the latter cases, but continue to grow over a large distance from the nozzle in the former case, leading to persistent large-scale coherent structures in the mixing layers for the jet with a laminar exit velocity profile.

We propose here to investigate the impact of small-scale effects on the bulk evolution of a two-phase flow system. More precisely, we choose to examine the sole influence of a small-scale (with respect to the bulk velocity) off-equilibrium velocity on the system. In order to narrow our analysis and avoid complex well-posedness issues, we choose to examine a simple barotropic 5-equation two-phase flow model that accounts for an equilibrium common bulk velocity and a small-scale off-equilibrium velocity. A full derivation of the model is presented: it is based on a variational principle which allows us to insert the two-scale kinematics into the model by considering two different kinetic energies. Additional entropy dissipation requirements allow us to add dissipative structures to the model. This system is neutral with respect to the topology of the flow structure and is equipped with parameters that can be connected to relaxation processes. When considering instantaneous relaxations, we obtain two limit systems of the literature that are used for the simulation of separated-phase flows. In this sense we obtain a hierarchy of models. We show that the parent 5-equation model is also compatible with the description of a bubbly fluid that allows small-scale vibrations for the disperse phase. This identification is verified and discussed through comparisons with experimental measurements of sound dispersion (Silberman, J. Acoust. Soc. Am., vol. 29, 1957, pp. 925–933; Leroy et al., J. Acoust. Soc. Am., vol. 123, 2008, pp. 1931–1940) and with the dispersion relations of a reference model for bubbly flows by Cheng et al. (Trans. ASME J. Heat Transfer, vol. 107, 1985, pp. 402–408). The present work is a first contribution to a larger effort that aims at unifying models that can describe both separated and disperse two-phase flows, coupling small-scale modelling with large-scale resolution.

Evolution of thermally stratified open channel flow after removal of a volumetric heat source is investigated using direct numerical simulation. The heat source models radiative heating from above and varies with height due to progressive absorption. After removal of the heat source the initial stable stratification breaks down and the channel approaches a fully mixed isothermal state. The initial state consists of three distinct regions: a near-wall region where stratification plays only a minor role, a central region where stratification has a significant effect on flow dynamics and a near-surface region where buoyancy effects dominate. We find that a state of local energetic equilibrium observed in the central region of the channel in the initial state persists until the late stages of the destratification process. In this region local turbulence parameters such as eddy diffusivity $k_{h}$ and flux Richardson number $R_{f}$ are found to be functions only of the Prandtl number $Pr$ and a mixed parameter ${\mathcal{Q}}$, which is equal to the ratio of the local buoyancy Reynolds number $Re_{b}$ and the friction Reynolds number $Re_{\unicode[STIX]{x1D70F}}$. Close to the top and bottom boundaries turbulence is also affected by $Re_{\unicode[STIX]{x1D70F}}$ and vertical position $z$. In the initial heated equilibrium state the laminar surface layer is stabilised by the heat source, which acts as a potential energy sink. Removal of the heat source allows Kelvin–Helmholtz-like shear instabilities to form that lead to a rapid transition to turbulence and significantly enhance the mixing process. The destratifying flow is found to be governed by bulk parameters $Re_{\unicode[STIX]{x1D70F}}$, $Pr$ and the friction Richardson number $Ri_{\unicode[STIX]{x1D70F}}$. The overall destratification rate ${\mathcal{D}}$ is found to be a function of $Ri_{\unicode[STIX]{x1D70F}}$ and $Pr$.

An extension to the classical shallow-water equation (SWE) is derived that exactly satisfies the bed condition and can be regarded as an approximation to wave scattering at the next order in the small parameter $(h/\unicode[STIX]{x1D706})^{2}$ (depth to wavelength ratio squared). In the frequency domain, the extended SWE shares the same simple structure as the standard SWE with coefficients modified by terms relating to the bed variation. In three dimensions the governing equation demonstrates that variable topography gives rise to anisotropic effects on wave scattering not present in the standard SWE, with consequences for the design of water wave metamaterials. Numerical examples illustrate that approximations to wave scattering using the extended SWE are significantly improved in comparison with the standard SWE.

The YBJ equation (Young & Ben Jelloul, J. Marine Res., vol. 55, 1997, pp. 735–766) provides a phase-averaged description of the propagation of near-inertial waves (NIWs) through a geostrophic flow. YBJ is obtained via an asymptotic expansion based on the limit 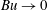$\mathit{Bu}\rightarrow 0$, where 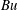$\mathit{Bu}$ is the Burger number of the NIWs. Here we develop an improved version, the YBJ+ equation. In common with an earlier improvement proposed by Thomas, Smith & Bühler (J. Fluid Mech., vol. 817, 2017, pp. 406–438), YBJ+ has a dispersion relation that is second-order accurate in 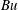$\mathit{Bu}$. (YBJ is first-order accurate.) Thus both improvements have the same formal justification. But the dispersion relation of YBJ+ is a Padé approximant to the exact dispersion relation and with 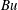$\mathit{Bu}$ of order unity this is significantly more accurate than the power-series approximation of Thomas et al. (2017). Moreover, in the limit of high horizontal wavenumber 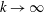$k\rightarrow \infty$, the wave frequency of YBJ+ asymptotes to twice the inertial frequency 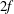$2f$. This enables solution of YBJ+ with explicit time-stepping schemes using a time step determined by stable integration of oscillations with frequency 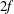$2f$. Other phase-averaged equations have dispersion relations with frequency increasing as 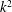$k^{2}$ (YBJ) or 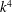$k^{4}$ (Thomas et al. 2017): in these cases stable integration with an explicit scheme becomes impractical with increasing horizontal resolution. The YBJ+ equation is tested by comparing its numerical solutions with those of the Boussinesq and YBJ equations. In virtually all cases, YBJ+ is more accurate than YBJ. The error, however, does not go rapidly to zero as the Burger number characterizing the initial condition is reduced: advection and refraction by geostrophic eddies reduces in the initial length scale of NIWs so that 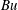$\mathit{Bu}$ increases with time. This increase, if unchecked, would destroy the approximation. We show, however, that dispersion limits the damage by confining most of the wave energy to low 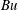$\mathit{Bu}$. In other words, advection and refraction by geostrophic flows does not result in a strong transfer of initially near-inertial energy out of the near-inertial frequency band.

The fluid dynamics of the collision and coalescence of liquid drops has intrigued scientists and engineers for more than a century owing to its ubiquitousness in nature, e.g. raindrop coalescence, and industrial applications, e.g. breaking of emulsions in the oil and gas industry. The complexity of the underlying dynamics, which includes occurrence of hydrodynamic singularities, has required study of the problem at different scales – macroscopic, mesoscopic and molecular – using stochastic and deterministic methods. In this work, a multi-scale, deterministic method is adopted to simulate the approach, collision, and eventual coalescence of two drops where the drops as well as the ambient fluid are incompressible, Newtonian fluids. The free boundary problem governing the dynamics consists of the Navier–Stokes system and associated initial and boundary conditions that have been augmented to account for the effects of disjoining pressure as the separation between the drops becomes of the order of a few hundred nanometres. This free boundary problem is solved by a Galerkin finite element-based algorithm. The interplay of inertial, viscous, capillary and van der Waals forces on the coalescence dynamics is investigated. It is shown that, in certain situations, because of inertia two drops that are driven together can first bounce before ultimately coalescing. This bounce delays coalescence and can result in the computed value of the film drainage time departing significantly from that predicted from existing scaling theories.