Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-19T13:00:51.714Z Has data issue: false hasContentIssue false
  • English
  • Français

On oblique liquid curtains

Published online by Cambridge University Press:  07 August 2019

Steven J. Weinstein Open the ORCID record for Steven J. Weinstein [Opens in a new window] ,
David S. Ross Open the ORCID record for David S. Ross [Opens in a new window] ,
Kenneth J. Ruschak Open the ORCID record for Kenneth J. Ruschak [Opens in a new window]  and
Nathaniel S. Barlow Open the ORCID record for Nathaniel S. Barlow [Opens in a new window]
Steven J. Weinstein*
Affiliation:
Department of Chemical Engineering, Rochester Institute of Technology, Rochester, NY 14623, USA School of Mathematical Sciences, Rochester Institute of Technology, Rochester, NY 14623, USA
David S. Ross
Affiliation:
School of Mathematical Sciences, Rochester Institute of Technology, Rochester, NY 14623, USA
Kenneth J. Ruschak
Affiliation:
Department of Chemical Engineering, Rochester Institute of Technology, Rochester, NY 14623, USA
Nathaniel S. Barlow
Affiliation:
School of Mathematical Sciences, Rochester Institute of Technology, Rochester, NY 14623, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In a recent paper (J. Fluid Mech., vol. 861, 2019, pp. 328–348), Benilov derived equations governing a laminar liquid sheet (a curtain) that emanates from a slot whose centreline is inclined to the vertical. The equations are valid for slender sheets whose characteristic length scale in the direction of flow is much larger than its cross-sectional thickness. For a liquid that leaves a slot with average speed, 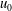$u_{0}$, volumetric flow rate per unit width, 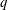$q$, surface tension, $\unicode[STIX]{x1D70E}$, and density, 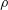$\unicode[STIX]{x1D70C}$, Benilov obtains parametric equations that predict steady-state curtain shapes that bend upwards against gravity provided 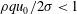$\unicode[STIX]{x1D70C}qu_{0}/2\unicode[STIX]{x1D70E}<1$. Benilov’s parametric equations are shown to be identical to those derived by Finnicum, Weinstein, and Ruschak (J. Fluid Mech., vol. 255, 1993, pp. 647–665). In the latter form, it is straightforward to deduce an alternative solution of Benilov’s equations where a curtain falls vertically regardless of the slot’s orientation. This solution is consistent with prior experimental and theoretical results that show that a liquid curtain can emerge from a slot at an angle different from that of the slot centreline.

JFM classification

Materials Processing Flows: Coating Interfacial Flows (free surface): Thin films
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , R3
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benilov, E. S. 2019 Oblique liquid curtains with a large Froude number. J. Fluid Mech. 861, 328–348.Google Scholar
Brown, D. R. 1961 A study of the behavior of a thin sheet of a moving liquid. J. Fluid Mech. 10, 297–305.Google Scholar
Clarke, A., Weinstein, S. J., Moon, A. G. & Simister, E. A. 1997 Time-dependent equations governing the shape of a two-dimensional liquid curtain. Part 2: Experiment. Phys. Fluids 9 (12), 3637–3644.Google Scholar
Finnicum, D. S., Weinstein, S. J. & Ruschak, K. J. 1993 The effect of applied pressure on the shape of a two-dimensional liquid curtain falling under the influence of gravity. J. Fluid Mech. 255, 647–665.Google Scholar
Girfoglio, M., De Rosa, F., Coppola, G. & de Luca, L. 2017 Unsteady critical liquid sheet flows. J. Fluid Mech. 821, 219–247.Google Scholar
John, F. 1982 Partial Differential Equations, 4th edn. Springer.Google Scholar
Keller, J. B. & Weitz, M. L. 1957 Upward ‘falling’ jets and surface tension. J. Fluid Mech. 2 (2), 201–203.Google Scholar
Weinstein, S. J., Clarke, A., Moon, A. G. & Simister, E. A. 1997 Time-dependent equations governing the shape of a two-dimensional liquid curtain. Part 1: Theory. Phys. Fluids 9 (12), 3625–3636.Google Scholar
Weinstein, S. J. & Ruschak, K. J. 1999 On the mathematical structure of thin film equations containing a critical point. Chem. Engng Sci. 54 (8), 977–985.Google Scholar
Weinstein, S. J. & Ruschak, K. J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29–53.Google Scholar