The effect of centrifugal force in turbulent rotating Rayleigh–Bénard convection (RRBC) is studied experimentally in an aspect-ratio $\varGamma =1$ cylindrical convection cell and in the ranges of the Froude number $0.004\leq Fr \leq 0.363$ and the Rayleigh number $2.8\times 10^8 \leq Ra \leq 9.5\times 10^9$, and with the Prandtl number fixed at $Pr=4.34$. We use the bulk temperature anomaly to determine the onset Froude number $Fr_c$, beyond which the centrifugal effects cannot be regarded as insignificant. It is found that $Fr_c$ depends on $Ra$ as $Fr_c\sim Ra^{0.53}$, which may be understood qualitatively by the idea of local force balance. For $Fr>Fr_c$, the centrifugal effect is more pronounced for smaller $Ra$, which is also found for larger constant $1/Ro$. This implies that the response of the system to the centrifugal force depends on the flow states, which, in RRBC, is mainly determined by the competition between the buoyancy and Coriolis forces. Detailed analysis of the sidewall temperature signal shows results consistent with those obtained from the bulk temperature. Based on the above results, we propose a different division of the $1/Ro$–$Fr$ phase space than previously suggested. For the heat transport, the results under fixed $1/Ro$ show well-defined $Nu$–$Ra$ scalings, which can provide a better prediction for the heat transport when extrapolating to the unexplored regions in the phase space.

The 2021 Nobel Prize in Physics recognizes advances in the understanding of complex systems, and underscores that ‘complex’ does not mean ‘imponderable’.

This work investigates nonlinear dimensionality reduction as a means of improving the accuracy and stability of reduced-order models of advection-dominated flows. Nonlinear correlations between temporal proper orthogonal decomposition (POD) coefficients can be exploited to identify latent low-dimensional structure, approximating the attractor with a minimal set of driving modes and a manifold equation for the remaining modes. By viewing these nonlinear correlations as an invariant manifold reduction, this least-order representation can be used to stabilize POD–Galerkin models or as a state space for data-driven model identification. In the latter case, we use sparse polynomial regression to learn a compact, interpretable dynamical system model from the time series of the active modal coefficients. We demonstrate this perspective on a quasiperiodic shear-driven cavity flow and show that the dynamics evolves on a torus generated by two independent Stuart–Landau oscillators. The specific approach to nonlinear correlations analysis used in this work is applicable to periodic and quasiperiodic flows, and cannot be applied to chaotic or turbulent flows. However, the results illustrate the limitations of linear modal representations of advection-dominated flows and motivate the use of nonlinear dimensionality reduction more broadly for exploiting underlying structure in reduced-order models.

We significantly extend the results of Miles & Sneyd (J. Fluid Mech., vol. 497, 2003, pp. 435–439) for an accelerating line load on a floating ice plate in their simple linear mathematical model by proceeding to numerical calculations for the response due to a decelerating load. Our results show: (i) how the deflections produced by an impulsively started steadily moving line load begin to develop and eventually approach the well-known steady load-speed-dependent quasi-static and wave-like forms, including above the shallow water gravity wave speed where the shadow zone evolves; (ii) the singularity in the deflection predicted in the simple linear model when the load moves steadily is indeed avoided by a uniformly accelerating load, where the magnitude of the deflection continually increases and its maximum lags a little further behind as the load moves through the critical speed and beyond; (iii) there is also no singularity in the deflection due to a uniformly decelerating load, but whereas the response from a subcritical starting speed is preserved and travels with the load, the magnitude of the deflection may become quite large near a load starting from supercritical speed and approaching rest, which is attributed to constructive interference (reinforcement) as erstwhile trailing, predominantly gravity, waves catch up with the load. While this reinforcement poses no risk to Hercules transport aircraft landing on the thick sea ice at McMurdo Sound, it can account for the reported rapid sinking of the detached cockpit shortly after it came to rest in the 1974 Lockheed Electra aircraft crash in the Canadian Arctic.

Biological and artificial microswimmers often encounter fluid media with non-Newtonian rheological properties. In particular, many biological fluids such as blood and mucus are shear-thinning. Recent studies have demonstrated how shear-thinning rheology can impact substantially the propulsion performance in different manners. In this work, we examine the effect of geometrical shape upon locomotion in a shear-thinning fluid using a prolate spheroidal squirmer model. We use a combination of asymptotic analysis and numerical simulations to quantify how particle geometry impacts the speed and the energetic cost of swimming. The results demonstrate the advantages of spheroidal over spherical swimmers in terms of both swimming speed and energetic efficiency when squirming through a shear-thinning fluid. More generally, the findings suggest the possibility of tuning the swimmer geometry to better exploit non-Newtonian rheological behaviours for more effective locomotion in complex fluids.

Water patch topology and momentum loss resulting from a jet impacting on the underside of a flat plate with varied hydrophobicity were studied. The jet's Reynolds and Froude numbers ranged from 3700 to 31 000, and from 1 to 23, respectively. Hence effects of gravity were expected to be non-negligible, and data suggest that this is the case for hydrophobic surfaces. The interplay of gravity, surface tension, inertia and viscosity resulted in two distinct behaviours. On hydrophilic surfaces, water spread uniformly. Friction reduced momentum, and led to accumulation at the edges of the patch until gravity overcame surface tension and produced droplets. On hydrophobic surfaces, two rims formed, enclosing a thin laminar film. The patch shape was mostly determined by the balance of kinetic and surface energy. Dewetting occurred in most cases when the two rims merged, but for a narrow parameter, range water detached soon after impact and formed a type of skewed water bell. The transition in detachment topology was predicted reasonably by a simple model considering whether an attached or detached rim minimizes energy. Due to promotion of dewetting by gravity, the water patch area decreased compared to that reported in previous studies, which considered jet impingement on vertical surfaces and tops of horizontal surfaces. Owing to the application that motivated this study, the streamwise force on the plate was also measured. On hydrophobic surfaces the reduction in force correlated with the reduction in water patch area. Water patch area and momentum loss were both found to scale best with the contact-angle-modified Weber number.

We take a complex systems approach to investigating experimentally the collective dynamics of a network of four self-excited thermoacoustic oscillators coupled in a ring. Using synchronization metrics, we find a wide variety of emergent multi-scale behaviour, such as (i) a transition from intermittent frequency locking on a $\mathbb {T}^{3}$ quasiperiodic attractor to a breathing chimera, (ii) a two-cluster state of anti-phase synchronization on a periodic limit cycle, and (iii) a weak anti-phase chimera. We then compute the cross-transitivity from recurrence networks to identify the dominant direction of the coupling between the heat-release-rate ($q^{\prime }_{\mathbb {X}}$) and pressure ($p^{\prime }_{\mathbb {X}}$) fluctuations in each individual oscillator, as well as that between the pressure ($p^{\prime }_{\mathbb {X}}$ and $p^{\prime }_{\mathbb {Y}}$) fluctuations in each pair of coupled oscillators. We find that networks of non-identical oscillators exhibit circumferentially biased $p^{\prime }_{\mathbb {X}}$–$p^{\prime }_{\mathbb {Y}}$ coupling, leading to mode localization, whereas networks of identical oscillators exhibit globally symmetric $p^{\prime }_{\mathbb {X}}$–$p^{\prime }_{\mathbb {Y}}$ coupling. In both types of networks, we find that the $p^{\prime }_{\mathbb {X}}$–$q^{\prime }_{\mathbb {X}}$ coupling can be symmetric or asymmetric, but that the asymmetry is always such that $q^{\prime }_{\mathbb {X}}$ exerts a greater influence on $p^{\prime }_{\mathbb {X}}$ than vice versa. Finally, we show through a cluster analysis that the $p^{\prime }_{\mathbb {X}}$–$p^{\prime }_{\mathbb {Y}}$ interactions play a more critical role than the $p^{\prime }_{\mathbb {X}}$–$q^{\prime }_{\mathbb {X}}$ interactions in defining the collective dynamics of the system. As well as providing new insight into the interplay between the $p^\prime_{\mathbb{X}}\text{--}p^\prime_{\mathbb{Y}}$ and $p^\prime_{\mathbb{X}}\text{--}q^\prime_{\mathbb{X}}$ coupling, this study shows that even a small network of four ring-coupled thermoacoustic oscillators can exhibit a wide variety of collective dynamics. In particular, we present the first evidence of chimera states in a minimal network of coupled thermoacoustic oscillators, paving the way for the application of oscillation quenching strategies based on chimera control.

The interaction of a droplet with a swirling airstream is investigated experimentally using shadowgraphy and particle image velocimetry techniques. In swirl flow, the droplet experiences oppose-flow, cross-flow and co-flow conditions depending on its ejection location, the velocity of the airstream and the swirl strength, which results in distinct droplet morphologies as compared with the straight airflow situation. We observe a new breakup phenomenon, termed as ‘retracting bag breakup’, as the droplet encounters a differential flow field created by the wake of the swirler's vanes and the central recirculation zone in swirl airflow. A regime map demarcating the various modes, such as no breakup, vibrational breakup, retracting bag breakup and bag breakup modes, is presented for different sets of dimensionless parameters influencing the droplet morphology and its trajectory. In contrast to the straight flow, the swirl flow promotes the development of the Rayleigh–Taylor instability, enhancing the stretching factor in the droplet deformation process, resulting in a larger number of fingers on the droplet's surface. In order to gain physical insight, a modified theoretical analysis based on the Rayleigh–Taylor instability is proposed for the swirl flow. The experimental behaviour of droplet deformation phenomena in swirl flow conditions can be determined by modifying the stretching factor in the theoretical model.

A theory of non-homogeneous turbulence is developed and applied to boundary-free shear flows. The theory introduces assumptions of inner and outer similarity for the non-homogeneity of two-point statistics, and predicts power-law scalings of second-order structure functions that have some similarities with but also some differences from Kolmogorov scalings. These scalings arise as a consequence of these assumptions, of the general interscale and interspace energy balance, and of an inner–outer equivalence hypothesis for turbulence dissipation. They reduce to the usual Kolmogorov scalings in stationary homogeneous turbulence. Comparisons with structure function data from three qualitatively different turbulent wakes provide support for the theory's predictions but also raise new questions for future research.

Boundary layer transition over a lifting body of 1.6 m length at $2^\circ$ angle of attack has been simulated at Mach 6 and a unit Reynolds number $1.0 \times 10^7$ m$^{-1}$. The model geometry is the same as the Hypersonic Transition Research Vehicle designed by the China Aerodynamics Research and Development Center. Four distinct transitional regions are identified, i.e. windward vortex region, shoulder vortex region, windward cross-flow region and shoulder cross-flow region. Multi-dimensional linear stability analyses by solving the two-dimensional eigenvalue problem (spatial BiGlobal approach) and the plane-marching parabolized stability equations (PSE3D approach) are further carried out to uncover the dominant instabilities in the last three regions as well as the shoulder attachment-line region. The shoulder vortex is conducive to both inner and outer modes of shear-layer instability, of which the latter most likely trigger the vortex breakdown. A novel method is presented to substantially reduce the computational cost of BiGlobal and PSE3D in resolving the cross-flow instabilities in cross-flow regions. The peak frequencies of cross-flow modes lie between 15 and 45 kHz. Whereas oblique second Mack modes are marginally unstable in the windward cross-flow region, they could be strong enough to compete with the cross-flow modes in the shoulder cross-flow region. In the shoulder attachment-line region, there exists only one unstable mode of Mack instability, differing from previous studies that show a hierarchy of modes in the context of symmetrical attachment-line flows. Results of the numerical simulation and multi-dimensional stability analyses are compared when possible, showing a fair agreement between the two approaches and highlighting the necessity of considering non-parallel effects.

The aim of the present study is to investigate the linear and nonlinear wave dynamics of a falling incompressible viscous fluid when the fluid undergoes an effect of odd viscosity. In fact, such an effect arises in classical fluids when the time-reversal symmetry is broken. The motivation to study this dynamics was raised by recent studies (Ganeshan & Abanov, Phys. Rev. Fluids, vol. 2, 2017, p. 094101; Kirkinis & Andreev, J. Fluid Mech., vol. 878, 2019, pp. 169–189) where the odd viscosity coefficient suppresses thermocapillary instability. Here, we explore the linear surface wave and shear wave dynamics for the isothermal case by solving the Orr–Sommerfeld eigenvalue problem numerically with the aid of the Chebyshev spectral collocation method. It is found that surface and shear instabilities can be weakened by the odd viscosity coefficient. Furthermore, the growth rate of the wavepacket corresponding to the linear spatio-temporal response is reduced as long as the odd viscosity coefficient increases. In addition, a coupled system of a two-equation model is derived in terms of the fluid layer thickness 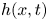$h(x,t)$ and the flow rate 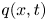$q(x,t)$. The nonlinear travelling wave solution of the two-equation model reveals the attenuation of maximum amplitude and speed in the presence of an odd viscosity coefficient, which ensures the delay of transition from the primary parallel flow with a flat surface to secondary flow generated through the nonlinear wave interactions. This physical phenomenon is further corroborated by performing a nonlinear spatio-temporal simulation when a harmonic forcing is applied at the inlet.

The transient pressure field around a moderately thick airfoil is studied as it undergoes ramp-type pitching motions at high Reynolds numbers and low Mach numbers. A unique set of laboratory experiments were performed in a high-pressure wind tunnel to investigate dynamic stall at chord Reynolds numbers in the range of $0.5\times 10^6\leq Re _c\leq 5.5\times 10^6$ in the absence of compressibility effects. In addition to variations of mean angle and amplitude, pitching manoeuvres at reduced frequencies in the range of $0.01\leq k\leq 0.40$ were studied by means of surface-pressure measurements. Independently of the parameter variations, all test cases exhibit a nearly identical stall behaviour characterized by a gradual trailing-edge stall, in which the dynamic stall vortex forms approximately at mid-chord. The location of the pitching window with respect to the Reynolds-number-dependent static stall angle is found to define the temporal development of the stall process. The time until stall onset is characterized by a power law, where a small excess of the static stall angle results in a drastically prolonged stall delay. The reduced frequency exhibits a decrease in impact on the stall development in the case of angle-limited pitching manoeuvres. Beyond a critical reduced frequency, both load magnitudes and vortex evolution become reduced frequency independent and instead depend on the geometry of the motion and the convective time scale, respectively. Overall, the characteristics of vortex evolution induced by dynamic stall show remarkable similarities to the framework of optimal vortex formation reported in Gharib et al. (J. Fluid Mech., vol. 360, 1998, pp. 121–140). The data from this study are publicly available at https://doi.org/10.34770/b3vq-sw14.

Meandering channels are dynamic landforms that arise as a result of fluid mechanic and sedimentary processes. Their evolution has been described by the meander-morphodynamic equations, which dictate that channel curvature and bed topography give rise to local perturbations in streamwise fluid velocity, prompting the preferential erosion and sediment deposition that constitute meander behaviour. Novel mathematical conditions are presented to guarantee unique solutions for the linearized equations in non-periodic domains with finite boundaries. With the boundary condition specification sufficient for the uniqueness proof one finds a well-posed initial-boundary-value problem amenable to standard numerical techniques for partial differential equations. This provides a pathway for improved numerical algorithms for simulations of meandering river dynamics. Previous theoretical analysis for linear stability theory in meandering dynamics has been restricted to spatially periodic systems. The present effort develops new results for linear stability theory in non-periodic systems with temporal driving at system boundaries as well as non-homogeneous initial conditions. Predictions for temporal driving at the inlets for non-periodic finite domains provide clarification for observed behaviour in laboratory flumes where driven conditions at the inlet avoids the long-term decay of all meanders observed in flumes with fixed entry conditions. Linear stability theory for finite domains confirms that a continuous perturbation is required for sustained meandering. Original scaling arguments are presented for the dependence of the meander migration rate on geological parameters, showing that the rate of channel migration increases with increased width, downreach slope and bank erodibility, and decreases with increased volumetric flow rate.

We consider the entrainment volume that results from the quasi-two-dimensional interactions of rising surface-parallel vorticity with an air–water interface. Based on systematic (three-dimensional) direct numerical simulations (DNS) of the canonical problem of a rectilinear vortex pair impinging on and entraining air at the free surface, we develop a phenomenological model to predict the resulting entrainment volume in terms of four key parameters. We identify a new parameter, a circulation flux Froude number $Fr^2_\Xi =|\varGamma |W/a^2\,g$, that predicts the dimensionless volume $\forall$ of entrained air initiated by a coherent vortical structure of circulation $\varGamma$, effective radius $a$, vertical rise velocity $W$ with gravity $g$. For $Fr^2_\Xi$ below some critical value $Fr^2_{\Xi cr}$, no air is entrained. For $Fr^2_\Xi >Fr^2_{\Xi cr}$, the average initial entrainment $\overline {\forall }_o$ scales linearly with ($Fr^2_\Xi -Fr^2_{\Xi cr}$). We also find that $\overline {\forall }_o$ is linearly dependent on circulation Weber number $We_{\varGamma }$ for a range of vortex Bond number $5 \lesssim Bo_{\varGamma } \lesssim 50$, and parabolically dependent on circulation Reynolds $Re_{\varGamma }$ for $Re_{\varGamma }\lesssim 2580$. Outside of these ranges, surface tension and viscosity have little effect on the initial entrainment volume. For the canonical rectilinear vortex problem, the simple model predicts $\overline {\forall }_o$ extremely well for individual coherent structures over broad ranges of $Fr^2_\Xi$, $We_{\varGamma }$, $Bo_{\varGamma }$ and $Re_{\varGamma }$. We evaluate the performance of this parameterisation and phenomenological entrainment model for air entrainment due to the complex periodic vortex shedding and quasi-steady wave breaking behind a fully submerged horizontal circular cylinder. For the range of parameters we consider, the phenomenological model predicts the event-by-event dimensionless entrainment volume measured in the DNS satisfactorily for this complex application.

We explore basic mechanisms for the instability of finite-amplitude interfacial gravity waves through a two-dimensional linear stability analysis of the periodic and irrotational plane motion of the interface between two unbounded homogeneous fluids of different density in the absence of background currents. The flow domains are conformally mapped into two half-planes, where the time-varying interface is always mapped onto the real axis. This unsteady conformal mapping technique with a suitable representation of the interface reduces the linear stability problem to a generalized eigenvalue problem, and allows us to accurately compute the growth rates of unstable disturbances superimposed on steady waves for a wide range of parameters. Numerical results show that the wave-induced Kelvin–Helmholtz (KH) instability due to the tangential velocity jump across the interface produced by the steady waves is the major instability mechanism. Any disturbances whose dominant wavenumbers are greater than a critical value grow exponentially. This critical wavenumber that depends on the steady wave steepness and the density ratio can be approximated by a local KH stability analysis, where the spatial variation of the wave-induced currents is neglected. It is shown, however, that the growth rates need to be found numerically with care and the successive collisions of eigenvalues result in the wave-induced KH instability. In addition, the present study extends the previous results for the small-wavenumber instability, such as modulational instability, of relatively small-amplitude steady waves to finite-amplitude ones.

We present an experimental investigation of the flow structure in the near wake of a NACA0012 airfoil plunging sinusoidally at a chord Reynolds number of Re = 20 000 and for a wide range of reduced frequency k and Strouhal number based on peak-to-peak amplitude St. Estimated mean thrust coefficients using the mean and fluctuating velocity fields confirm the St2 dependence as well as a significant effect of the reduced frequency for k ≤ 1. Generally, time-averaged flow quantities are better correlated with St than k in the range tested (k ≤ 3.14 and St ≤ 0.24). Analysis of the streamwise flow and cross-flow in the near wake using two-point cross-correlations and proper orthogonal decomposition reveals that the unsteady characteristics are even better correlated with St than the mean flow quantities. The percentage energy of the fundamental wake modes of the streamwise flow and the flapping mode of the cross-flow increases with increasing St, but at different rates in the drag-producing and thrust-producing wakes. There are similarities to the wake synchronisation behind oscillating bodies. The spanwise-averaged cross-correlation coefficient in the measurement domain grows linearly for small St (in drag-producing wakes), and is nearly constant at a high value for larger St (in thrust-producing wakes). Results show that the Strouhal number is the most important parameter that determines the degree of two-dimensionality of the wake, and suggest that spanwise vortices are quasi-two-dimensional for St ≥ 0.05 and x/c ≤ 4. The implications for experimental gust generators using oscillating airfoils are discussed.

We report experimental and theoretical results on how a fluid (homogeneous or continuously stratified) is spun up in a closed, semicircular cylinder. Experiments were performed for Rossby numbers $Ro=0.02$, 0.2 and 1 (the latter corresponding to the limiting case of spin-up from rest), with the Ekman number $E=O({10^{-5}})$, and the Burger number ($S$) varied between 0 and 10. There are two key processes: Ekman pumping that drives the core flow; and the formation and breakdown of the vertical-wall boundary layers, with respective characteristic time scales $t\sim E^{-1/2}$ and $Ro^{-1}$. When these time scales are comparable, the observed flow is dominated by the gradual spin-up of the initial anticyclone that forms when the rotation rate is increased, which fills the container's interior; vorticity generated adjacent to the vertical walls throughout remains confined to the neighbourhood of the container's walls and corners. Conversely, when ${E^{1/2}/Ro\ll 1}$, the vertical-wall boundary layers rapidly break down, resulting in the formation of cyclonic vortices in the container's vertical corners, which grow and interact with the initial anticyclone, leading to the formation of a three-cell flow pattern. For $Ro=0.02$, our theoretical description of the flow generally agrees well with experiments, and the computation of the eruption times for the unsteady boundary layers is consistent with the observations for both $Ro=0.02$ and $Ro=0.2$.

Large-eddy simulations of turbulent flow in partially filled pipes are conducted to investigate the effect of secondary currents on the friction factor, first- and second-order statistics and large-scale turbulent motion. The method is validated first and simulated profiles of the mean streamwise velocity, normal stresses and turbulent kinetic energy (TKE) are shown to be in good agreement with experimental data. The secondary flow is stronger in half- and three-quarters full pipes compared with quarter full or fully filled pipe flows, respectively. The origin of the secondary flow is examined by both the TKE budget and the steamwise vorticity equation, providing evidence that secondary currents originate from the corner between the free surface and the pipe walls, which is where turbulence production is larger than the sum of the remaining terms of the TKE budget. An extra source of streamwise vorticity production is found at the free surface near the centreline bisector, due to the two-component asymmetric turbulence there. The occurrence of dispersive stresses (due to secondary currents) reduces the contribution of the turbulent shear stress to the friction factor, which results in a reduction of the total friction factor of flows in half and three-quarters full pipes in comparison to a fully filled pipe flow. Furthermore, the presence of significant secondary currents inhibits very-large-scale motion (VLSM), which in turn reduces the strength and scales of near-wall streaks. Subsequently, near-wall coherent structures generated by streak instability and transient growth are significantly suppressed. The absence of VLSM and less coherent near-wall turbulence structures is supposedly responsible for the drag reduction in partially filled pipe flows relative to a fully filled pipe flow at an equivalent Reynolds number.

The behaviour of a fully rough-wall turbulent boundary layer subjected to different pressure gradients is investigated for different Reynolds numbers using hot-wire measurements. Mean velocity and velocity root-mean-square measurements indicate that the boundary layer remains in a self-preserving state regardless of the pressure gradient. However, different pressure gradients lead to different self-preservation states, as suggested by the lack of collapse of the velocity profile between the pressure gradient cases. The results also indicate that the roughness effect is more important than the pressure gradient; particularly, the closer the wall, the more dominant the roughness effect over the pressure gradient effect on the boundary layer. Finally, both spectral and proper orthogonal decomposition analyses applied to the hot-wire measurements indicate that the pressure gradient impacts predominantly the large-scale motion.

We develop coupled evolution equations for viscous fingering (VF) and phase separation in partially miscible systems by combining a simple double-well thermodynamic free energy and Korteweg force with a classical miscible VF model for a binary system. The VF pattern transition into a droplet formation pattern by the spinodal decomposition effect is demonstrated, and the simultaneous increases in the depth of the energy minimum, in the difference in the equilibrium concentrations, and in the Korteweg force, enhance the droplet growth. The pattern's interfacial length increases with the spinodal decomposition effects. These results match the corresponding experimental results.