Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chu, Xin
Chang, Long
Jia, Beinan
and
Jian, Yongjun
2022.
Effect of the odd viscosity on Faraday wave instability.
Physics of Fluids,
Vol. 34,
Issue. 11,
Desai, Akshay S.
Chattopadhyay, Souradip
and
Gaonkar, Amar K.
2023.
Shear imposed falling liquid films on a slippery substrate with Marangoni effects: Effect of odd viscosity.
International Journal of Non-Linear Mechanics,
Vol. 156,
Issue. ,
p.
104507.
Chu, Xin
and
Jian, Yongjun
2023.
Electrostatically induced Faraday instability of thin film with spontaneous odd viscosity.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 314,
Issue. ,
p.
105013.
Kadry, Zakaria
2023.
Bifurcation of traveling waves in a liquid film with broken time-reversal symmetry.
Physics Letters A,
Vol. 477,
Issue. ,
p.
128895.
Zakaria, Kadry
and
Alsharif, Abdullah M.
2023.
Dynamics of a liquid sheet with a broken time reversal.
Alexandria Engineering Journal,
Vol. 65,
Issue. ,
p.
1031.
Chattopadhyay, Souradip
Desai, Akshay S.
Gaonkar, Amar K.
and
Mukhopadhyay, Anandamoy
2023.
Role of odd viscosity on falling films over compliant substrates.
Physical Review Fluids,
Vol. 8,
Issue. 6,
Samanta, Arghya
2023.
An elliptic velocity profile-based two-equation model in viscous film.
Physics of Fluids,
Vol. 35,
Issue. 2,
Desai, Akshay S.
Chattopadhyay, Souradip
Gaonkar, Amar K.
Barua, Amlan K.
and
Mukhopadhyay, Anandamoy
2023.
Suppression of Wave Instability in a Liquid Film Flow Down a Non-Uniformly Heated Slippery Inclined Plane Using Odd Viscosity.
Journal of Fluids Engineering,
Vol. 145,
Issue. 9,
Chattopadhyay, Souradip
and
Ji, Hangjie
2023.
Thermocapillary thin film flows on a slippery substrate with odd viscosity effects.
Physica D: Nonlinear Phenomena,
Vol. 455,
Issue. ,
p.
133883.
Desai, Akshay S.
Chattopadhyay, Souradip
Gaonkar, Amar K.
and
Mukhopadhyay, Anandamoy
2023.
Shear imposed falling film with odd viscosity effects.
International Journal of Non-Linear Mechanics,
Vol. 153,
Issue. ,
p.
104422.
Hossain, Md. Mouzakkir
Tsai, Chia-Cheng
and
Behera, Harekrushna
2023.
Instability mechanism of shear-layered fluid in the presence of a floating elastic plate.
Physics of Fluids,
Vol. 35,
Issue. 2,
Jia, Beinan
and
Jian, Yongjun
2023.
Stability of a liquid film on inclined flexible substrates: Effect of the spontaneous odd viscosity.
Physical Review E,
Vol. 108,
Issue. 4,
Yuan, Hang
and
Olvera de la Cruz, Monica
2023.
Stokesian dynamics with odd viscosity.
Physical Review Fluids,
Vol. 8,
Issue. 5,
Paul, Dipankar
Hossain, Md. Mouzakkir
and
Behera, Harekrushna
2023.
Hydrodynamic instability of odd-viscosity-induced shear-imposed falling film.
Physics of Fluids,
Vol. 35,
Issue. 3,
Fruchart, Michel
Scheibner, Colin
and
Vitelli, Vincenzo
2023.
Odd Viscosity and Odd Elasticity.
Annual Review of Condensed Matter Physics,
Vol. 14,
Issue. 1,
p.
471.
Yang, Jingyang
Du, Shaofeng
Xiao, Yue
Wang, Shaowei
Zhao, Moli
and
Xiong, QingRong
2024.
Instability of odd viscosity falling liquid films with insoluble surfactants.
Physics of Fluids,
Vol. 36,
Issue. 8,
Hossain, Md. Mouzakkir
Ghosh, Sukhendu
and
Behera, Harekrushna
2024.
Odd-viscosity induced surfactant-laden shear-imposed viscous film over a slippery incline: a stability analysis.
Meccanica,
Vol. 59,
Issue. 9,
p.
1381.
Paul, Dipankar
Hossain, Md. Mouzakkir
and
Behera, Harekrushna
2024.
Hydrodynamic stability analysis of shear-layered fluid flow over a porous bed in the presence of a floating elastic plate.
International Journal of Non-Linear Mechanics,
Vol. 159,
Issue. ,
p.
104599.
Chattopadhyay, Souradip
2024.
Falling liquid film down a non-uniformly heated slippery inclined plane with odd viscosity effects.
International Journal of Heat and Mass Transfer,
Vol. 218,
Issue. ,
p.
124807.
Desai, Akshay S.
Chattopadhyay, Souradip
and
Gaonkar, Amar K.
2024.
Falling liquid films on a uniformly heated compliant substrate with broken time-reversal symmetry.
Journal of Fluids and Structures,
Vol. 125,
Issue. ,
p.
104064.
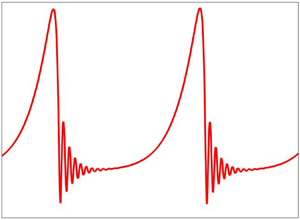
 $h(x,t)$ and the flow rate
$h(x,t)$ and the flow rate  $q(x,t)$. The nonlinear travelling wave solution of the two-equation model reveals the attenuation of maximum amplitude and speed in the presence of an odd viscosity coefficient, which ensures the delay of transition from the primary parallel flow with a flat surface to secondary flow generated through the nonlinear wave interactions. This physical phenomenon is further corroborated by performing a nonlinear spatio-temporal simulation when a harmonic forcing is applied at the inlet.
$q(x,t)$. The nonlinear travelling wave solution of the two-equation model reveals the attenuation of maximum amplitude and speed in the presence of an odd viscosity coefficient, which ensures the delay of transition from the primary parallel flow with a flat surface to secondary flow generated through the nonlinear wave interactions. This physical phenomenon is further corroborated by performing a nonlinear spatio-temporal simulation when a harmonic forcing is applied at the inlet.