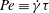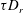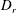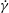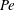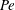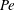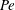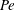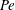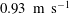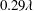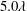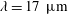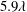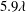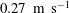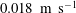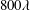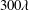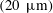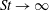Identifying the convective/absolute instability nature of a local base flow requires an analysis of its linear impulse response. One must find the appropriate singularity in the eigenvalue problem with complex frequencies and wavenumbers and prove causality. One way to do so is to show that the appropriate integration contour of this response, a steepest decent path through the relevant singularity, exists. Due to the inherent difficulties of such a proof, one often verifies instead whether this singularity satisfies the collision criterion. In other words, one must show that the branches involved in the formation of this singularity come from distinct halves of the complex wavenumber plane. However, this graphical search is computationally intensive in a single plane and essentially prohibitive in two planes. A significant computational cost reduction can be achieved when root finding procedures are applied instead of graphical ones to search for singularities. They focus on locating these points, with causality being verified graphically a posteriori for a small parametric sample size. The use of root-finding procedures require auxiliary equations, often derived by applying the zero group velocity conditions to the dispersion relation. This relation, in turn, is derived by applying matrix forming to the differential eigenvalue problem and taking the determinant of the resulting system of algebraic equations. Taking the derivative of the dispersion relation with respect to the wavenumbers generates the auxiliary equations. If the algebraic system is decoupled, this derivation is straightforward. However, its computational cost is often prohibitive when the algebraic system is coupled. Other methods exist, but often they can also be too costly and/or not reliable for two wavenumber plane searches. This paper describes an alternative methodology based on sensitivity analysis and adjoints that allow the zero group velocity conditions to be applied directly to the differential eigenvalue problem. In doing so, the direct and auxiliary differential eigenvalue problems can be solved simultaneously using standard shooting methods to directly locate singularities. Auxiliary dispersion relations no longer have to be derived, although it is shown that they are the algebraic equivalent of the auxiliary differential eigenvalue problems obtained by this alternative methodology. Using the latter dramatically reduces computational costs. The search for arbitrary singularities is then not only accelerated in single wavenumber planes but it also becomes viable in two wavenumber planes. Finally, the new method also allows group velocity calculations, greatly facilitating the verification of causality. Several test cases are presented to illustrate the capabilities of this new method.

In many shear- and pressure-driven wall-bounded turbulent flows secondary motions spontaneously develop and their interaction with the main flow alters the overall large-scale features and transfer properties. Taylor–Couette flow, the fluid motion developing in the gap between two concentric cylinders rotating at different angular velocities, is not an exception, and toroidal Taylor rolls have been observed from the early development of the flow up to the fully turbulent regime. In this manuscript we show that under the generic name of ‘Taylor rolls’ there is a wide variety of structures that differ in the vorticity distribution within the cores, the way they are driven and their effects on the mean flow. We relate the rolls at high Reynolds numbers not to centrifugal instabilities, but to a combination of shear and anti-cyclonic rotation, showing that they are preserved in the limit of vanishing curvature and can be better understood as a pinned cycle which shows similar characteristics as the self-sustained process of shear flows. By analysing the effect of the computational domain size, we show that this pinning is not a product of numerics, and that the position of the rolls is governed by a random process with the space and time variations depending on domain size.

Data-driven decompositions are becoming essential tools in fluid dynamics, allowing for tracking the evolution of coherent patterns in large datasets, and for constructing low-order models of complex phenomena. In this work, we analyse the main limits of two popular decompositions, namely the proper orthogonal decomposition (POD) and the dynamic mode decomposition (DMD), and we propose a novel decomposition which allows for enhanced feature detection capabilities. This novel decomposition is referred to as multi-scale proper orthogonal decomposition (mPOD) and combines multi-resolution analysis (MRA) with a standard POD. Using MRA, the mPOD splits the correlation matrix into the contribution of different scales, retaining non-overlapping portions of the correlation spectra; using the standard POD, the mPOD extracts the optimal basis from each scale. After introducing a matrix factorization framework for data-driven decompositions, the MRA is formulated via one- and two-dimensional filter banks for the dataset and the correlation matrix respectively. The validation of the mPOD, and a comparison with the discrete Fourier transform (DFT), DMD and POD are provided in three test cases. These include a synthetic test case, a numerical simulation of a nonlinear advection–diffusion problem and an experimental dataset obtained by the time-resolved particle image velocimetry (TR-PIV) of an impinging gas jet. For each of these examples, the decompositions are compared in terms of convergence, feature detection capabilities and time–frequency localization.

Bidimensional empirical mode decomposition (BEMD) is used to identify attached eddies in turbulent channel flows and quantify their relationship with the mean skin-friction drag generation. BEMD is an adaptive, non-intrusive, data-driven method for mode decomposition of multiscale signals especially suitable for non-stationary and nonlinear processes such as those encountered in turbulent flows. In the present study, we decompose the velocity fluctuations obtained by direct numerical simulation of channel flows into BEMD modes characterized by specific length scales. Unlike previous works (e.g. Flores & Jiménez, Phys. Fluids, vol. 22(7), 2010, 071704; Hwang, J. Fluid Mech., vol. 767, 2015, pp. 254–289), the current approach employs naturally evolving wall-bounded turbulence without modifications of the Navier–Stokes equations to maintain the inherent turbulent dynamics, and minimize artificial numerical enforcement or truncation. We show that modes identified by BEMD exhibit a self-similar behaviour, and that single attached eddies are mainly composed of streaky structures carrying intense streamwise velocity fluctuations and vortex packets permeating in all velocity components. Our findings are consistent with the existence of attached eddies in actual wall-bounded flows, and show that BEMD modes are tenable candidates to represent Townsend attached eddies. Finally, we evaluate the turbulent-drag generation from the perspective of attached eddies with the aid of the Fukagata–Iwamoto–Kasagi identity (Fukagata et al., Phys. Fluids, vol. 14(11), 2002, pp. L73–L76) by splitting the Reynolds shear stress into four different terms related to the length scale of the attached eddies.

This paper follows a recent article of Nambiar et al. (J. Fluid Mech., vol. 812, 2017, pp. 41–64) on the linear rheological response of a dilute bacterial suspension (e.g. E. coli) to impulsive starting and stopping of simple shear flow. Here, we analyse the time dependent nonlinear rheology for a pair of linear flows – simple shear (a canonical weak flow) and uniaxial extension (a canonical strong flow), again in response to impulsive initiation and cessation. The rheology is governed by the bacterium orientation distribution which satisfies a kinetic equation that includes rotation by the imposed flow, and relaxation to isotropy via rotary diffusion and tumbling. The relevant dimensionless parameters are the Péclet number 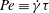$Pe\equiv \dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D70F}$, which dictates the importance of flow-induced orientation anisotropy, and 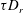$\unicode[STIX]{x1D70F}D_{r}$, which quantifies the relative importance of the two intrinsic orientation decorrelation mechanisms (tumbling and rotary diffusion). Here, $\unicode[STIX]{x1D70F}$ is the mean run duration of a bacterium that exhibits a run-and-tumble dynamics, 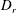$D_{r}$ is the intrinsic rotary diffusivity of the bacterium and 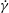$\dot{\unicode[STIX]{x1D6FE}}$ is the characteristic magnitude of the imposed velocity gradient. The solution of the kinetic equation is obtained numerically using a spectral Galerkin method, that yields the rheological properties (the shear viscosity, the first and second normal stress differences for simple shear, and the extensional viscosity for uniaxial extension) over the entire range of 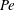$Pe$. For simple shear, we find that the stress relaxation predicted by our analysis at small 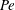$Pe$ is in good agreement with the experimental observations of Lopez et al. (Phys. Rev. Lett., vol. 115, 2015, 028301). However, the analysis at large 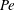$Pe$ yields relaxations that are qualitatively different. Upon step initiation of shear, the rheological response in the experiments corresponds to a transition from a nearly isotropic suspension of active swimmers at small 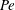$Pe$, to an apparently (nearly) isotropic suspension of passive rods at large 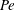$Pe$. In contrast, the computations yield the expected transition to a nearly flow-aligned suspension of passive rigid rods at high 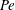$Pe$. We probe this active–passive transition systematically, complementing the numerical solution with analytical solutions obtained from perturbation expansions about appropriate base states. Our study suggests courses for future experimental and analytical studies that will help understand relaxation phenomena in active suspensions.

A phenomenological theory of diffusion and cross-diffusion of tracer particles in concentrated hard-sphere suspensions is developed. Expressions for the diffusion coefficients as functions of the host particle volume fraction are obtained up to the close-packing limit. In concentrated systems the tracer diffusivity decreases because of the reduced pore space available for diffusion. The tracer diffusivity can be modelled by a Stokes–Einstein equation with an effective viscosity that depends on the pore size. Tracer diffusion and segregation during sedimentation cease at a critical trapping volume fraction corresponding to a tracer glass transition. The tracer cross-diffusion coefficient, however, increases near the glass transition and diverges in the close-packed limit.

The near-wall turbulent flow over a superhydrophobic surface (SHS) with random texture was studied using three-dimensional Lagrangian particle tracking velocimetry (3D-PTV). The channel was operated at a constant mass flow rate over the SHS and a smooth surface at a Reynolds number of 7000 based on the bulk velocity of $0.93~\text{m}~\text{s}^{-1}$ and the full channel height. The friction Reynolds number was 217, based on the friction velocity and half channel height. The 3D-PTV processing was based on the shake-the-box algorithm applied to images of fluorescent tracers recorded using four high-speed cameras. The SHS was obtained by spray coating, resulting in a root-mean-square roughness of $0.29\unicode[STIX]{x1D706}$ and an average texture width of $5.0\unicode[STIX]{x1D706}$, where $\unicode[STIX]{x1D706}=17~\unicode[STIX]{x03BC}\text{m}$ is the inner flow scale over the SHS. The 3D-PTV measurements confirmed an isotropic slip with a streamwise slip length of $5.9\unicode[STIX]{x1D706}$ and a spanwise slip length of $5.9\unicode[STIX]{x1D706}$. As a result, both the near-wall mean streamwise and spanwise velocity profiles over the SHS were higher than the smooth surface. The streamwise and spanwise slip velocities over the SHS were $0.27~\text{m}~\text{s}^{-1}$ and $0.018~\text{m}~\text{s}^{-1}$, respectively. The near-wall Reynolds stresses over the SHS were larger and shifted towards the wall when normalized by the corresponding inner scaling, despite the smaller friction Reynolds number of 180 over the SHS. The near-wall measurement of streamwise velocity showed that the shear-free pattern consists of streamwise-elongated regions with a length of $800\unicode[STIX]{x1D706}$ and a spanwise width of $300\unicode[STIX]{x1D706}$. The plastron dimensions correspond to the mean distance of the largest roughness peaks $(20~\unicode[STIX]{x03BC}\text{m})$ obtained from profilometry of the SHS. The drag reduction over the SHS was 30 %–38 % as estimated from pressure measurement and the flow field using the 3D-PTV.

The water film due to rain falling on a radome surface causes severe losses in radio wave transmission. Hydrophobic coatings have been applied as a remedy to reduce the film thickness and to minimize the losses. However, quantitative accounts of the wave scattering are mostly based on empirical estimates of the film thickness. We describe a fluid-mechanical theory for the film under steady rain falling on a textured surface formed by a square array of pillars. Assuming the water surface on top of the pillars to be in the Cassie–Baxter state, the analysis is carried out by making use of the sharp contrast of length scales between the film thickness and the radome radius. The textured surface is viewed as a periodic array of cells around pillars. The macro-scale flow is simple and linear but the micro-scale flow in a typical lattice period is fully nonlinear. These two problems are coupled and are solved iteratively to obtain the slip length and the spatial variation of the film thickness. Numerical results are presented to show the effect of solid fraction on local flow field, the slip length and the non-uniform reduction of the film thickness. To examine the influence of the macro-scale geometry on film formation, the theory is also modified for a hydrophobic roof top formed by two inclined planes.

A non-perturbative nonlinear theory for moderately dense gas–solid suspensions is outlined within the framework of the Boltzmann–Enskog equation by extending the work of Saha & Alam (J. Fluid Mech., vol. 833, 2017, pp. 206–246). A linear Stokes’ drag law is adopted for gas–particle interactions, and the viscous dissipation due to hydrodynamic interactions is incorporated in the second-moment equation via a density-corrected Stokes number. For the homogeneous shear flow, the present theory provides a unified treatment of dilute to dense suspensions of highly inelastic particles, encompassing the high-Stokes-number rapid granular regime ($St\rightarrow \infty$) and its small-Stokes-number counterpart, with quantitative agreement for all transport coefficients. It is shown that the predictions of the shear viscosity and normal-stress differences based on existing theories deteriorate markedly with increasing density as well as with decreasing Stokes number and restitution coefficient.