Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T16:30:50.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Streamwise and spanwise slip over a superhydrophobic surface

Published online by Cambridge University Press:  15 May 2019

Wagih Abu Rowin Open the ORCID record for Wagih Abu Rowin [Opens in a new window]  and
Sina Ghaemi Open the ORCID record for Sina Ghaemi [Opens in a new window]
Wagih Abu Rowin
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, Alberta T6G 2G8, Canada
Sina Ghaemi*
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, Alberta T6G 2G8, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The near-wall turbulent flow over a superhydrophobic surface (SHS) with random texture was studied using three-dimensional Lagrangian particle tracking velocimetry (3D-PTV). The channel was operated at a constant mass flow rate over the SHS and a smooth surface at a Reynolds number of 7000 based on the bulk velocity of 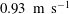$0.93~\text{m}~\text{s}^{-1}$ and the full channel height. The friction Reynolds number was 217, based on the friction velocity and half channel height. The 3D-PTV processing was based on the shake-the-box algorithm applied to images of fluorescent tracers recorded using four high-speed cameras. The SHS was obtained by spray coating, resulting in a root-mean-square roughness of 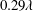$0.29\unicode[STIX]{x1D706}$ and an average texture width of 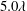$5.0\unicode[STIX]{x1D706}$, where 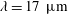$\unicode[STIX]{x1D706}=17~\unicode[STIX]{x03BC}\text{m}$ is the inner flow scale over the SHS. The 3D-PTV measurements confirmed an isotropic slip with a streamwise slip length of 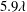$5.9\unicode[STIX]{x1D706}$ and a spanwise slip length of 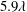$5.9\unicode[STIX]{x1D706}$. As a result, both the near-wall mean streamwise and spanwise velocity profiles over the SHS were higher than the smooth surface. The streamwise and spanwise slip velocities over the SHS were 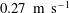$0.27~\text{m}~\text{s}^{-1}$ and 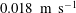$0.018~\text{m}~\text{s}^{-1}$, respectively. The near-wall Reynolds stresses over the SHS were larger and shifted towards the wall when normalized by the corresponding inner scaling, despite the smaller friction Reynolds number of 180 over the SHS. The near-wall measurement of streamwise velocity showed that the shear-free pattern consists of streamwise-elongated regions with a length of 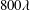$800\unicode[STIX]{x1D706}$ and a spanwise width of 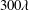$300\unicode[STIX]{x1D706}$. The plastron dimensions correspond to the mean distance of the largest roughness peaks 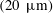$(20~\unicode[STIX]{x03BC}\text{m})$ obtained from profilometry of the SHS. The drag reduction over the SHS was 30 %–38 % as estimated from pressure measurement and the flow field using the 3D-PTV.

JFM classification

Boundary Layers: Boundary layer control Flow Control: Drag reduction Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 1127 - 1157
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abu Rowin, W., Hou, J. & Ghaemi, S. 2017 Inner and outer layer turbulence over a superhydrophobic surface with low roughness level at low Reynolds number. Phys. Fluids 29 (9), 095106.Google Scholar
Abu Rowin, W., Hou, J. & Ghaemi, S. 2018 Turbulent channel flow over riblets with superhydrophobic coating. Exp. Therm. Fluid. Sci. 94, 192–204.Google Scholar
Alame, K. & Mahesh, K.2018 Wall-bounded flow over a realistically rough superhydrophobic surface. J. Fluid Mech., in press.Google Scholar
Aljallis, E., Sarshar, M. A., Datla, R., Sikka, V. & Jon, A. 2013 Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 25, 025103.Google Scholar
Bechert, D., Brus, M., Hag, W., van der Hoeven, J. & Hopp, G. 1997 Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech. 338, 59–87.Google Scholar
Busse, A. & Sandham, N. D. 2012 Influence of an anisotropic slip-length boundary condition on turbulent channel flow. Phys. Fluids 24, 055111.Google Scholar
Choi, C. H., Ulmanella, U., Kim, J., Ho, C. M. & Kim, C. J. 2006 Effective slip and friction reduction in nanograted superhydrophobic microchannels. Phys. Fluids 18, 087105.Google Scholar
Clauser, F. H. 1956 The turbulent boundary layer. In Advances in Applied Mechanics, vol. 4, pp. 1–51. Elsevier.Google Scholar
Daniello, R. J., Waterhouse, N. E. & Rothstein, J. P. 2009 Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids 21, 085103.Google Scholar
Dean, R. B. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. Trans. ASME J. Fluids Engng 100 (2), 215–223.Google Scholar
Dilip, D., Jha, N. K., Govardhan, R. N. & Bobji, M. S. 2014 Controlling air solubility to maintain ‘Cassie’ state for sustained drag reduction. Colloids Surf. A 459, 217–224.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin-friction in wall-bounded flows. Phys. Fluids 14, L73–L76.Google Scholar
Fukagata, K., Kasagi, N. & Koumoutsakos, P. 2006 A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces. Phys. Fluids 18, 051703.Google Scholar
Gesemann, S., Huhn, F., Schanz, D. & Schröder, A. 2016 From noisy particle tracks to velocity, acceleration and pressure fields using B-splines and penalties. In 18th International Symposium on the Applications of Laser and Imaging Techniques to Fluid Mechanics (Lisbon, Portugal, 4–7 July).Google Scholar
Gilbert, N. & Kleiser, L. 1991 Turbulence model testing with the aid of direct numerical simulation results. In Proc. 8th Symposium on Turbulent Shear Flows, Sept. 9–11, Munich, Germany.Google Scholar
Gose, J. W., Golovin, K., Boban, M., Mabry, J. M., Tuteja, A., Perlin, M. & Ceccio, S. L. 2018 Characterization of superhydrophobic surfaces for drag reduction in turbulent flow. J. Fluid Mech. 845, 560–580.Google Scholar
Hughes, I. & Hase, T. 2010 Measurements and their Uncertainties: A Practical Guide to Modern Error Analysis, pp. 37–51. Oxford University Press.Google Scholar
Joseph, P., Cottin-Bizonn, C., Benot, J.-M., Ybert, C., Journet, C., Tabeling, P. & Bocquet, L. 2006 Slippage of water past superhydrophobic carbon nanotube forests in microchannels. Phys. Rev. Lett. 97 (15), 156104.Google Scholar
Kähler, C. J., Scharnowski, S. & Cierpka, C. 2012 On the uncertainty of digital PIV and PTV near walls. Exp. Fluids 52 (6), 1641–1656.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Lee, J., Jelly, T. O. & Zaki, T. A. 2015 Effect of Reynolds number on turbulent drag reduction by superhydrophobic surface textures. Flow Turbul. Combust. 95, 277–300.Google Scholar
Lei, L., Li, H., Shi, J. & Chen, Y. 2009 Diffraction patterns of a water-submerged superhydrophobic grating under pressure. Langmuir 26 (5), 3666–3669.Google Scholar
Ling, H.2017 Experimental investigation of friction drag reduction in turbulent boundary layer by super-hydrophobic surfaces. Doctoral dissertation, Johns Hopkins University.Google Scholar
Ling, H., Katz, J., Fu, M. & Hultmark, M. 2017 High-resolution velocity measurement in the inner part of turbulent boundary layers over super-hydrophobic surfaces. J. Fluid Mech. 801, 670–703.Google Scholar
Ling, H., Srinivasan, S., Golovin, K., McKinley, G. H., Tuteja, A. & Katz, J. 2016 Effect of Reynolds number and saturation level on gas diffusion in and out of a superhydrophobic surface. Phys. Rev. Fluids 801, 670–703.Google Scholar
Martell, M. B., Perot, J. B. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31–41.Google Scholar
Martell, M. B., Rothstein, J. P. & Perot, J. B. 2010 An analysis of superhydrophobic turbulent drag reduction mechanisms using direct numerical simulation. Phys. Fluids 22, 065102.Google Scholar
Min, T. & Kim, J. 2004 Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 16, L55–L58.Google Scholar
Novara, M., Schanz, D., Reuther, N., Kähler, C. J. & Schröder, A. 2016 Lagrangian 3D particle tracking in high-speed flows: shake-the-box for multi-pulse systems. Exp. Fluids 57, 128.Google Scholar
Ou, J., Perot, J. B. & Rothstein, J. 2004 Laminar drag reduction in microchannels using superhydrophobic surfaces. Phys. Fluids 16 (12), 4635–4643.Google Scholar
Ou, J. & Rothstein, J. 2005 Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys. Fluids 17 (10), 103606.Google Scholar
Park, H., Park, H. & Kim, J. 2013 A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25, 110815.Google Scholar
Park, H., Sun, G. & Kim, C.-J. 2014 Superhydrophobic turbulent drag reduction as a function of surface grating parameters. J. Fluid Mech. 747, 722–734.Google Scholar
Rastegari, A. & Akhavan, R. 2015 On the mechanism of turbulent drag reduction with superhydrophobic surfaces. J. Fluid Mech. 773, R4.Google Scholar
Rastegari, A. & Akhavan, R. 2019 On drag reduction scaling and sustainability bounds of superhydrophobic surfaces in high Reynolds number turbulent flows. J. Fluid Mech. 864, 327–347.Google Scholar
Reholon, D & Ghaemi, S. 2018 Plastron morphology and drag of a superhydrophobic surface in turbulent regime. Phys. Rev. Fluids 3 (10), 104003.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Samaha, M. A., Tafreshi, H. V. & Gad-El-Hak, M. 2012 Influence of flow on longevity of superhydrophobic coatings. Langmuir 28, 9759–9766.Google Scholar
Scarano, F. 2012 Tomographic PIV: principles and practice. Meas. Sci. Technol. 24 (1), 012001.Google Scholar
Schanz, D., Gesemann, S., Schröder, A., Wienek, B. & Novara, M. 2012 Non-uniform optical transfer functions in particle imaging: calibration and application to tomographic reconstruction. Meas. Sci. Technol. 24 (2), 024009.Google Scholar
Schanz, D., Schröder, A., Gesemann, S. & Wienek, B. 2013 ‘Shake the box’: a highly efficient and accurate tomographic particle tracking velocimetry (TOMO-PTV) method using prediction of particle positions. In 10th International Symposium on Particle Image Velocimetry. Delft, The Netherlands.Google Scholar
Schanz, D., Gesemann, S. & Schröder, A. 2016 Shake-the-box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57, 70.Google Scholar
Schröder, A., Schanz, D., Geisler, R., Gesemann, S. & Willert, C. 2015 Near-wall turbulence characterization using 4D-PTV shake-the-box. In 11th International Symposium on Particle Image Velocimetry–PIV15. Santa Barbara, California, 14–16 Sept 2015.Google Scholar
Seo, J., García-Mayoral, R. & Mani, A. 2018 Turbulent flows over superhydrophobic surfaces: flow-induced capillary waves, and robustness of air–water interfaces. J. Fluid Mech. 835, 45–85.Google Scholar
Seo, J. & Mani, A. 2018 Effect of texture randomization on the slip and interfacial robustness in turbulent flows over superhydrophobic surfaces. Phys. Rev. Fluids. 3 (4), 044601.Google Scholar
Türk, S., Daschiel, G., Stroh, A., Hasegawa, Y. & Frohnapfel, B. 2014 Turbulent flow over superhydrophobic surfaces with streamwise grooves. J. Fluid Mech. 747, 186–217.Google Scholar
Vajdi Hokmabad, B. & Ghaemi, S. 2016 Turbulent flow over wetted and non-wetted superhydrophobic counterparts with random structure. Phys. Fluids 28 (1), 015112.Google Scholar
Vajdi Hokmabad, B. & Ghaemi, S. 2017 Effect of flow and particle–plastron collision on the longevity of superhydrophobicity. Sci. Rep. 7, 41448.Google Scholar
Vinuesa, R., Noorani, A., Lozano-Durán, A., Khoury, G. K. E., Schlatter, P., Fischer, P. F. & Nagib, H. M. 2014 Aspect ratio effects in turbulent duct flows studied through direct numerical simulation. J. Turbul. 15 (10), 677–706.Google Scholar
Voth, G. A., La Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.Google Scholar
Wieneke, B. 2008 Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 45 (4), 549–556.Google Scholar
Wieneke, B. 2012 Iterative reconstruction of volumetric particle distribution. Meas. Sci. Technol. 24 (2), 024008.Google Scholar
Woolford, B., Princ, J., Maynes, D. & Webb, B. W. 2009 Particle image velocimetry characterization of turbulent channel flow with rib patterned superhydrophobic walls. Phys. Fluids 21, 085106.Google Scholar
Young, T. 1805 An essay on the cohesion of fluids. Phil. Trans. R. Soc. Lond. 95, 65–87.Google Scholar
Zhang, J., Tian, H., Yao, Z., Hao, P. & Jiang, N. 2015 Mechanisms of drag reduction of superhydrophobic surfaces in a turbulent boundary layer flow. Exp. Fluids 56, 179.Google Scholar