Papers
Shear-induced breaking of large internal solitary waves
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 1-29
-
- Article
- Export citation
Direct numerical simulations of turbulent flows over superhydrophobic surfaces
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 31-41
-
- Article
- Export citation
Downstream flow condition effects on the RR → MR transition of asymmetric shock waves in steady flows
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 43-62
-
- Article
- Export citation
MTV measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 63-88
-
- Article
- Export citation
Steady separated flow past a circular cylinder at low Reynolds numbers
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 89-119
-
- Article
- Export citation
Geometry of enstrophy and dissipation, grid resolution effects and proximity issues in turbulence
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 121-166
-
- Article
- Export citation
Boundary between unsteady and overturning ship bow wave regimes
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 167-175
-
- Article
- Export citation
Homogenized Euler equation: a model for compressible velocity gradient dynamics
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 177-194
-
- Article
- Export citation
Effects of wavelength and amplitude of a wavy cylinder in cross-flow at low Reynolds numbers
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 195-220
-
- Article
- Export citation
On nonlinear wave groups and crest statistics
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 221-239
-
- Article
- Export citation
Macro-scale description of transient electro-kinetic phenomena over polarizable dielectric solids
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 241-262
-
- Article
- Export citation
Input–output analysis, model reduction and control of the flat-plate boundary layer
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 263-298
-
- Article
- Export citation
Distribution of complex phase velocities for small disturbances to pipe Poiseuille flow
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 299-312
-
- Article
- Export citation
Drift and deformation of oil slicks due to surface waves
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 313-332
-
- Article
- Export citation
Dynamics of drop coalescence at fluid interfaces
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 333-352
-
- Article
- Export citation
Nonlinear dynamics of viscoelastic Taylor–Couette flow: effect of elasticity on pattern selection, molecular conformation and drag
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 353-382
-
- Article
- Export citation
Large eddy simulation of a circular jet: effect of inflow conditions on the near field
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 383-411
-
- Article
- Export citation


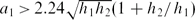 , while stable waves were on or below this limit. Breaking ISWs were investigated for 0.27 <
, while stable waves were on or below this limit. Breaking ISWs were investigated for 0.27 < 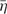
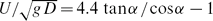 with g ≡ acceleration of gravity. These measurements of bow wave unsteadiness provide preliminary experimental validation of the foregoing simple theoretical relation for the boundary between the unsteady and overturning bow wave regimes for non-bulbous wedge-shaped ship bows with insignificant rake and flare. Extension of this relation to more complicated ship bows, notably bows with rake and flare, is also considered.
with g ≡ acceleration of gravity. These measurements of bow wave unsteadiness provide preliminary experimental validation of the foregoing simple theoretical relation for the boundary between the unsteady and overturning bow wave regimes for non-bulbous wedge-shaped ship bows with insignificant rake and flare. Extension of this relation to more complicated ship bows, notably bows with rake and flare, is also considered.