Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-22T14:43:38.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Shear-induced breaking of large internal solitary waves

Published online by Cambridge University Press:  10 February 2009

DORIAN FRUCTUS ,
MAGDA CARR ,
JOHN GRUE ,
ATLE JENSEN  and
PETER A. DAVIES
DORIAN FRUCTUS
Affiliation:
Mechanics Division, Department of Mathematics, University of Oslo, PO Box 1053, Blindern, 0316 Oslo, Norway
MAGDA CARR
Affiliation:
School of Mathematics and Statistics, University of St Andrews, Fife KY16 9SS, UK.
JOHN GRUE*
Affiliation:
Mechanics Division, Department of Mathematics, University of Oslo, PO Box 1053, Blindern, 0316 Oslo, Norway
ATLE JENSEN
Affiliation:
Mechanics Division, Department of Mathematics, University of Oslo, PO Box 1053, Blindern, 0316 Oslo, Norway
PETER A. DAVIES
Affiliation:
Department of Civil Engineering, The University, Dundee DD1 4HN, UK.
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability properties of 24 experimentally generated internal solitary waves (ISWs) of extremely large amplitude, all with minimum Richardson number less than 1/4, are investigated. The study is supplemented by fully nonlinear calculations in a three-layer fluid. The waves move along a linearly stratified pycnocline (depth h2) sandwiched between a thin upper layer (depth h1) and a deep lower layer (depth h3), both homogeneous. In particular, the wave-induced velocity profile through the pycnocline is measured by particle image velocimetry (PIV) and obtained in computation. Breaking ISWs were found to have amplitudes (a1) in the range 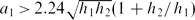, while stable waves were on or below this limit. Breaking ISWs were investigated for 0.27 < h2/h1 < 1 and 4.14 < h3/(h1 + h2) < 7.14 and stable waves for 0.36 < h2/h1 < 3.67 and 3.22 < h3/(h1 + h2) < 7.25. Kelvin–Helmholtz-like billows were observed in the breaking cases. They had a length of 7.9h2 and a propagation speed 0.09 times the wave speed. These measured values compared well with predicted values from a stability analysis, assuming steady shear flow with U(z) and ρ(z) taken at the wave maximum (U(z) horizontal velocity profile, ρ(z) density along the vertical z). Only unstable modes in waves of sufficient strength have the chance to grow sufficiently fast to develop breaking: the waves that broke had an estimated growth (of unstable modes) more than 3.3–3.7 times than in the strongest stable case. Evaluation of the minimum Richardson number (Rimin, in the pycnocline), the horizontal length of a pocket of possible instability, with wave-induced Ri < 14, (Lx) and the wavelength (λ), showed that all measurements fall within the range Rimin = −0.23Lx/λ + 0.298 ± 0.016 in the (Lx/λ, Rimin)-plane. Breaking ISWs were found for Lx/λ > 0.86 and stable waves for Lx/λ < 0.86. The results show a sort of threshold-like behaviour in terms of Lx/λ. The results demonstrate that the breaking threshold of Lx/λ = 0.86 was sharper than one based on a minimum Richardson number and reveal that the Richardson number was found to become almost antisymmetric across relatively thick pycnoclines, with the minimum occurring towards the top part of the pycnocline.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 620 , 10 February 2009 , pp. 1 - 29
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alexakis, A. 2005 On Holmboe's instability for smooth shear and density profiles. Phys. Fluids 17, 84–103.CrossRefGoogle Scholar
Bogucki, D. & Garrett, C. 1993 A simple model for the shear-induced decay of an internal solitary wave. J. Phys. Oceanogr. 23, 1767–1776.2.0.CO;2>CrossRefGoogle Scholar
Carpenter, J. R., Lawrence, G. A., & Smyth, W. D. 2007 Evolution and mixing of asymmetric Holmboe instabilities. J. Fluid Mech. 582, 103–132.CrossRefGoogle Scholar
Carr, M., Fructus, D., Grue, J., Jensen, A. & Davies, P. A. 2008 Convectively-induced shear instability in large internal solitary waves. Phys. Fluids 20, 12660.CrossRefGoogle Scholar
Caulfield, C. P. & Peltier, W. R. 2000 Three dimensionalization of the stratified mixing layer. Phys. Fluid 413, 1–47.Google Scholar
Dalziel, S. B. 2006 Digiflow user guide. http://www.dampt.cam.ac.uk/lab/digiflow/.Google Scholar
Duda, T. F., Lynch, J. F., Irish, J. D., Beardsley, R. C. & Ramp, S. R. 2004 Internal tide and nonlinear wave behaviour in the continental slope in the northern South China Sea. IEEE J. Ocean Engng 29, 1105–31.CrossRefGoogle Scholar
Fringer, O. B. & Street, R. L. 2003 The dynamics of breaking progressive interfacial waves. J. Fluid Mech. 494, 319–353.CrossRefGoogle Scholar
Fructus, D. & Grue, J. 2004 Fully nonlinear solitary waves in a layered stratified fluid. J. Fluid Mech. 505, 323–347.CrossRefGoogle Scholar
Gardner, C. S., Greene, J. M., Kruskal, M. D. & Muira, R. M. 1967 Method for solving the Korteweg–de Vries equation. Phys. Rev. Lett. 19, 1095–1097.CrossRefGoogle Scholar
Grue, J. 2005 Generation, propagation, and breaking of internal solitary waves. Chaos 15, 037110–1–14.CrossRefGoogle ScholarPubMed
Grue, J. 2006 Very large internal waves in the ocean – observations and nonlinear models. In Waves in Geophysical Fluids – Tsunamis, Rogue Waves, Internal Waves and Internal Tides (ed. Grue, J. & Trulsen, K.), pp. 205–270. Springer.Google Scholar
Grue, J., Jensen, A., Rusås, P.-O. & Sveen, J. K. 1999 Properties of large-amplitude internal waves. J. Fluid Mech. 380, 257–278.CrossRefGoogle Scholar
Hazel, P. 1972 Numerical studies of the stability of inviscid stratified shear flows. J. Fluid Mech. 51, 39–61.CrossRefGoogle Scholar
Helfrich, K. R. & Melville, W. K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38, 395–425.CrossRefGoogle Scholar
Hogg, A. M. & Ivey, G. N. 2003 The Kelvin–Helmholtz to Holmboe instability transition in stratified exchange flows. J. Fluid Mech. 477, 339–362.CrossRefGoogle Scholar
Holmboe, J. 1962 On the behaviour of symmetric waves in stratified shear layers. Geophys. Publ. 24, 67–112.Google Scholar
Howard, L. N. 1961 Note on a paper by John W. Miles. J. Fluid Mech. 10, 509–512.CrossRefGoogle Scholar
Kao, T. W., Pan, F.-S. & Renouard, D. 1985 Internal solitons on the pycnocline: generation, propagation, and shoaling and breaking over a slope. J. Fluid Mech. 159:19–53.CrossRefGoogle Scholar
Michallet, H. & Bartélemy, 1998 Experimental study of interfacial solitary waves. J. Fluid Mech. 366, 159–177.CrossRefGoogle Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.CrossRefGoogle Scholar
Moum, J. N., Farmer, D. M., Smyth, W. D., Armi, L. & Vagle, S. 2003 Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf. J. Phys. Oceanogr. 33, 2093–2112.2.0.CO;2>CrossRefGoogle Scholar
Ostrovsky, L. A. & Grue, J. 2003 Evolution equations for strongly nonlinear internal waves. Phys. Fluids 15 (10), 2934–2948.CrossRefGoogle Scholar
Ostrovsky, L. A. & Stepanyants, Y. A. 2005 Internal solitons in laboratory experiments. Chaos 15, 037111–1–28.CrossRefGoogle ScholarPubMed
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.CrossRefGoogle Scholar
Scotti, R. S. & Corcos, G. M. 1972 An experiment on the stability of small disturbances in a stratified free shear layer. J. Fluid Mech. 52, 499–528.CrossRefGoogle Scholar
Smyth, W. D., Nash, J. D. & Moum, J. N. 2005 Differential diffusion in breaking Kelvin–Helmholtz billows. J. Phys. Oceanogr. 35, 1004–1022.CrossRefGoogle Scholar
Stanton, T. P. & Ostrovsky, L. A. 1998 Observations of highly nonlinear internal solitons over the continental shelf. Geophys. Res. Lett. 25 (14), 2695–2698.CrossRefGoogle Scholar
Staquet, C. 2000 Mixing in a stably stratified shear layer: two- and three-dimensional numerical experiments. Fluid Dyn. Res. 27, 367–404.CrossRefGoogle Scholar
Sveen, J. K., Guo, & Grue, J. 2002 On the breaking of internal solitary waves at a ridge. J. Fluid Mech. 469, 161–188.CrossRefGoogle Scholar
Troy, C. D. & Koseff, J. R. 2005 The instability and breaking of long internal waves. J. Fluid Mech. 543, 107–136.CrossRefGoogle Scholar
Tung, K.-K., Chan, T. F. & Kubota, T. 1982 Large amplitude internal waves of permanent form. Stud. Appl. Math. 66, 1–44.CrossRefGoogle Scholar
Turkington, B., Eydeland, A. & Wang, S. 1991 A computational method for solitary internal waves in a continuously stratified fluid. Stud. Appl. Math. 85, 93–127.CrossRefGoogle Scholar
Zhu, D. Z. & Lawrence, G. A. 2001 Holmboe's instability in exchange flows. J. Fluid Mech. 429, 391–409.CrossRefGoogle Scholar