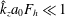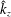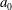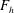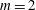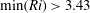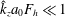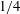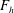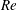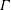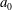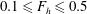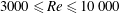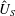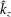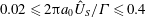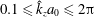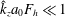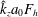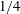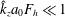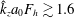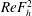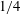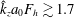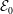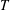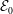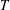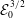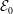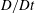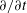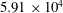In this paper, we investigate the dynamics of an initially vertical vortex embedded in a shear flow in a stratified fluid by means of a long-wavelength analysis. The main goal is to determine, whether or not, the Kelvin–Helmholtz instability can develop unconditionally as speculated by Lilly (J. Atmos. Sci., vol. 40, 1983, pp. 749–761). The analysis is performed in the case of the Lamb–Oseen vortex profile and a shear flow uniform in the horizontal and varying sinusoidally along the vertical using the assumption 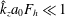$\hat{k}_{z}a_{0}F_{h}\ll 1$, where 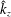$\hat{k}_{z}$ is the vertical wavenumber, 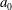$a_{0}$ the vortex radius and 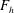$F_{h}$ the horizontal Froude number based on the circulation of the vortex. The results show that the vortex axis is advected not only in the direction of the shear flow but also in the perpendicular direction owing to the self-induced motion of the vortex. In addition, internal waves are transiently excited at the beginning, generating an initial non-hydrostatic regime. Their relative effects on the displacements of the vortex axis are weak except initially. The angular velocity of the vortex decays owing to a dynamic effect and viscous effects related to the vertical shear. The former effect is due to the squeezing of isopycnals in the vortex core, which implies a decrease of the vertical vorticity to satisfy potential vorticity conservation. In addition, a horizontal velocity field with an azimuthal wavenumber 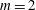$m=2$ is generated, meaning that the shape of the vortex becomes slightly elliptical. We further show that the minimum asymptotic Richardson number is bounded, 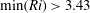$\min (Ri)>3.43$, when 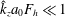$\hat{k}_{z}a_{0}F_{h}\ll 1$ and therefore cannot go below the critical value 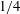$1/4$. This is because the growth of the vertical shear of the horizontal velocity of the vortex saturates owing to the decay of its angular velocity and because the squeezing of isopycnals increases the stratification strength. This suggests that the shear instability cannot always develop in strongly stratified flows, contrary to the conjecture of Lilly (as above). These predictions will be tested against direct numerical simulations in Part 2.

We conduct direct numerical simulations of an initially vertical Lamb–Oseen vortex in an ambient shear flow varying sinusoidally along the vertical in a stratified fluid. The Froude number $F_{h}$ and the Reynolds number $Re$, based on the circulation $\unicode[STIX]{x1D6E4}$ and radius $a_{0}$ of the vortex, have been varied in the ranges: $0.1\leqslant F_{h}\leqslant 0.5$ and $3000\leqslant Re\leqslant 10\,000$. The shear flow amplitude $\hat{U} _{S}$ and vertical wavenumber $\hat{k}_{z}$ lie in the ranges: $0.02\leqslant 2\unicode[STIX]{x03C0}a_{0}\hat{U} _{S}/\unicode[STIX]{x1D6E4}\leqslant 0.4$ and $0.1\leqslant \hat{k}_{z}a_{0}\leqslant 2\unicode[STIX]{x03C0}$. The results are analysed in the light of the asymptotic analyses performed in Part $1$. The vortex is mostly advected in the direction of the shear flow but also in the perpendicular direction owing to the self-induction. The decay of potential vorticity is strongly enhanced in the regions of high shear. The long-wavelength analysis for $\hat{k}_{z}a_{0}F_{h}\ll 1$ predicts very well the deformations of the vortex axis. The evolutions of the vertical shear of the horizontal velocity and of the vertical gradient of the buoyancy at the location of maximum shear are also in good agreement with the asymptotic predictions when $\hat{k}_{z}a_{0}F_{h}$ is sufficiently small. As predicted by the asymptotic analysis, the minimum Richardson number never goes below the critical value $1/4$ when $\hat{k}_{z}a_{0}F_{h}\ll 1$. The numerical simulations show that the shear instability is triggered only when $\hat{k}_{z}a_{0}F_{h}\gtrsim 1.6$ for sufficiently high buoyancy Reynolds number $ReF_{h}^{2}$. There is also a weak dependence of this threshold on the shear flow amplitude. In agreement with the numerical simulations, the long-wavelength analysis predicts that the minimum Richardson number goes below $1/4$ when $\hat{k}_{z}a_{0}F_{h}\gtrsim 1.7$ although this is beyond its expected range of validity.

A study of dense-gas effects on the stability of compressible boundary-layer flows is conducted. From the laminar similarity solution, the temperature variations are small due to the high specific heat of dense gases, leading to velocity profiles close to the incompressible ones. Concurrently, the complex thermodynamic properties of dense gases can lead to unconventional compressibility effects. In the subsonic regime, the Tollmien–Schlichting viscous mode is attenuated by compressibility effects and becomes preferentially skewed in line with the results based on the ideal-gas assumption. However, the absence of a generalized inflection point precludes the sustainability of the first mode by inviscid mechanisms. On the contrary, the viscous mode can be completely stable at supersonic speeds. At very high speeds, we have found instances of radiating supersonic instabilities with substantial amplification rates, i.e. waves that travel supersonically relative to the free-stream velocity. This acoustic mode has qualitatively similar features for various thermodynamic conditions and for different working fluids. This shows that the leading parameters governing the boundary-layer behaviour for the dense gas are the constant-pressure specific heat and, to a minor extent, the density-dependent viscosity. A satisfactory scaling of the mode characteristics is found to be proportional to the height of the layer near the wall that acts as a waveguide where acoustic waves may become trapped. This means that the supersonic mode has the same nature as Mack’s modes, even if its frequency for maximal amplification is greater. Direct numerical simulation accurately reproduces the development of the supersonic mode and emphasizes the radiation of the instability waves.

The endothelial glycocalyx layer (EGL) is a brush-like layer that lines the internal surfaces of blood vessels. It is thought to serve a number of physiological functions, including as a mechanotransducer of fluid loadings to the vessel wall. However, the fragility of the EGL makes it difficult to examine experimentally, and so there is much value in theoretical models that can help to explain the dynamical behaviour of the EGL. Most previous models have employed mixture theory to mechanically describe the layer, which treats the EGL as a isotropic linearly poroelastic layer. However, there is increasing experimental evidence to suggest that the EGL has a well-defined organisational structure that might not necessarily be well captured by such mixture theory descriptions. We therefore employ homogenisation theory to incorporate into the models some of the possible EGL microstructure suggested by the current biological literature. We explore how mechanotransduction varies under the different possible EGL microstructures, which potentially has important consequences to our understanding of how structural changes to the EGL might affect a vessel’s ability to respond to hemodynamical cues. We also find that, whereas mechanotransduction through the solid components of the EGL is dominated by the fluid tractions applied at the lumen–EGL interface, the component carried through its fluid phase is most sensitive to pressure gradients within the bulk EGL. This is relevant, since it is known that the underlying endothelial cells respond differently to these two different forms of mechanical loading.

Phase-resolved wave simulation and direct numerical simulation of turbulence are performed to investigate the surface wave effects on the energy transfer in overlying turbulent flow. The JONSWAP spectrum is used to initialize a broadband wave field. The nonlinear wave field is simulated using a high-order spectral method, and the resultant wave surface provides the bottom boundary conditions for direct numerical simulation of the overlying turbulent flow. Two wave ages of $c_{p}/u_{\ast }=2$ and 25 are considered, corresponding to slow and fast wave fields, respectively, where $c_{p}$ denotes the celerity of the peak wave and $u_{\ast }$ denotes the friction velocity. The energy transfer of turbulent motions in the presence of surface waves is investigated through the spectral analysis of the two-point correlation transport equation. It is found that the production term has an extra peak at the dominant wavelength scale in the vicinity of the surface, and the energy transported to the surface via viscous and spatial turbulent transport is enhanced in the region of $y^{+}<10$. The presence of surface waves results in an inverse turbulent energy cascade in the near-surface region, where small-scale wave-related motions transfer energy back to the dominant wavelength scale. Pressure-related terms reflecting the spatial and inter-component energy transfer are strongly dependent on the wave age. Furthermore, triadic interaction analysis reveals that the energy influx at the dominant wavelength scale is due to the contribution of the neighbouring streamwise turbulent motions, and those at the harmonic wavelength scales contribute the most.

This investigation concerns a systematic search for potentially singular behaviour in three-dimensional (3-D) Navier–Stokes flows. Enstrophy serves as a convenient indicator of the regularity of solutions to the Navier Stokes system – as long as this quantity remains finite, the solutions are guaranteed to be smooth and satisfy the equations in the classical (pointwise) sense. However, there are no estimates available with finite a priori bounds on the growth of enstrophy and, hence, the regularity problem for the 3-D Navier–Stokes system remains open. In order to quantify the maximum possible growth of enstrophy, we consider a family of optimization problems in which initial conditions with prescribed enstrophy ${\mathcal{E}}_{0}$ are sought such that the enstrophy in the resulting Navier–Stokes flow is maximized at some time $T$. Such problems are solved computationally using a large-scale adjoint-based gradient approach derived in the continuous setting. By solving these problems for a broad range of values of ${\mathcal{E}}_{0}$ and $T$, we demonstrate that the maximum growth of enstrophy is in fact finite and scales in proportion to ${\mathcal{E}}_{0}^{3/2}$ as ${\mathcal{E}}_{0}$ becomes large. Thus, in such a worst-case scenario the enstrophy still remains bounded for all times and there is no evidence for formation of singularity in finite time. We also analyse properties of the Navier–Stokes flows leading to the extreme enstrophy values and show that this behaviour is realized by a series of vortex reconnection events.

Fluid motion has two well-known fundamental processes: the vector transverse process characterized by vorticity, and the scalar longitudinal process consisting of a sound mode and an entropy mode, characterized by dilatation and thermodynamic variables. The existing theories for the sound mode involve the multi-variable issue and its associated difficulty of source identification. In this paper, we define the source of sound inside the fluid by the objective causality inherent in dynamic equations relevant to a longitudinal process, which naturally favours the material time-rate operator $D/Dt$ rather than the local time-rate operator $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$, and describes the sound mode by inhomogeneous advective wave equations. The sources of sound physical production inside the fluid are then examined at two levels. For the conventional formulation in terms of thermodynamic variables at the first level, we show that the universal kinematic source can be condensed to a scalar invariant of the surface deformation tensor. Further, in the formulation in terms of dilatation at the second level, we find that the sound mode in viscous and heat-conducting flow has sources from rich nonlinear couplings of vorticity, entropy and surface deformation, which cannot be disclosed at the first level. Preliminary numerical demonstration of the theoretical findings is made for two typical compressible flows, i.e. the interaction of two corotating Gaussian vortices and the unsteady type IV shock/shock interaction. The results obtained in this study provide a new theoretical basis for, and physical insight into, understanding various nonlinear longitudinal processes and the interactions therein.

We use interface-resolved direct numerical simulations to study the dynamics of a single sediment particle in a turbulent open channel flow over a fixed porous bed. The relative strength of the gravitational acceleration, quantified by the Galileo number, is varied so as to reproduce the different modes of sediment transport – resuspension, saltation and rolling. The results show that the sediment dynamics at lower Galileo numbers (i.e. resuspension and saltation) are mainly governed by the mean flow. Here, the regime of motion can be predicted by the ratio between the gravity and the shear-induced boundary force. In these cases, the sediment particle rapidly takes off when exposed to the flow, and proceeds with an oscillatory motion. Increasing the Galileo number, the frequency of these oscillations increases and their amplitude decreases, until the transport mode switches from resuspension to saltation. In this case, the sediment travels by short successive collisions with the bed. Further increasing the Galileo number, the particle rolls without detaching from the bed. Differently from the previous modes, the motion is triggered by extreme turbulent events, and the particle response depends on the specific initial conditions, at fixed Reynolds number. The results reveal that close to the onset of sediment motion, only turbulent sweeps can effectively trigger the particle motion by increasing the stagnation pressure upstream. We show that for the parameters in this study, a criterion based on the streamwise flow-induced force can successfully predict the incipient movement.

The Mach–Zehnder interferometer with the finite fringe method is applied for the first time to diagnose the three-dimensional density field of a shock-containing microjet issued from a convergent nozzle with an inner diameter of 1 mm at the exit. Experiments are performed at a nozzle pressure ratio of 4.0 to produce an underexpanded free jet with a Mach disk in the first shock-cell where the Reynolds number, based upon the diameter and flow properties at the nozzle exit, is $5.91\times 10^{4}$. Interferogram analyses for reconstructing the jet density fields are performed using the Abel inversion method, in which the analysis of the phase shift of the deformed fringe relative to the background fringe is carried out by the Fourier transform method. In addition to experiments, the flow field of the shock-containing microjet is simulated by solving the Reynolds-averaged Navier–Stokes equations with the SST $k$–$\unicode[STIX]{x1D714}$ turbulence model for a quantitative mutual comparison between the simulation and the experiment. The detailed variation of the density field associated with the Mach disk, the slip streams and the outer shear layers near the jet boundaries are successfully captured. Furthermore, the density profile along the jet centreline obtained by the present experiment is quantitatively compared with those from prior quantitative visualization studies, such as rainbow schlieren deflectometry, background oriented schlieren, moiré schlieren and Mach–Zehnder interferometer. The three-dimensional contour map coloured by the magnitude of the density gradient vector inside the microjet reveals the flow topology of the near-field shock systems and elucidates the spatial variation of the shock strength.

Transient electrohydrodynamics of a liquid drop at finite Reynolds numbers is studied by computer simulations. The governing equations of the problem are solved using a parallelized front tracking/finite difference method in the framework of the Taylor–Melcher leaky dielectric theory. The effect of the dielectric properties of the fluids on the dynamic response of the drop is studied by considering three representative fluid systems, which encompass all the regions of the deformation–circulation map. A parametric study is performed over a range of capillary number $Ca$, the Ohnesorge number squared $Oh^{2}$ and the viscosity ratio $\widetilde{\unicode[STIX]{x1D707}}$ to explore the effect of these parameters on the dynamic response. At low to intermediate capillary numbers, the dynamic response resembles that of a first- or second-order mechanical system, where the deformation settles to a steady state monotonically or through oscillations. However, beyond a threshold capillary number, the dynamic response becomes nonlinear. It is shown that the Ohnesorge number squared $Oh^{2}$ and the viscosity ratio $\widetilde{\unicode[STIX]{x1D707}}$ are the key parameters that determine the transition from a monotonic response to an oscillatory one (and vice versa) in density-matched fluid systems. To predict the dynamic response of nearly spherical drops at arbitrary $Oh^{2}$, an analytical equation is developed, which results in a critical Ohnesorge number squared $Oh_{c}^{2}$ that demarks a monotonic response from an oscillatory one. Investigations on the effect of the viscosity ratio $\widetilde{\unicode[STIX]{x1D707}}$ on the dynamic response shows that the relaxation time (for monotonic response) increases with an increase in $\widetilde{\unicode[STIX]{x1D707}}$ and that the steady state deformation ${\mathcal{D}}_{ss}$ correlates positively with $\widetilde{\unicode[STIX]{x1D707}}$ for oblate drops; however, depending on the corresponding regions of prolate drops on the deformation–circulation map, ${\mathcal{D}}_{ss}$ correlates positively or negatively with $\widetilde{\unicode[STIX]{x1D707}}$. A long-standing misconception regarding the oblate region is also rectified by development of a normal stress map, which determines the relative importance of the electric pressure and the normal hydrodynamic stress in setting the sense of the deformation of the drop.

We conduct Eulerian–Lagrangian simulations to study double-diffusive sedimentation in stratified flows. The results show the pattern of double-diffusive sedimentation and the transition to the pattern of Rayleigh–Taylor instability when the size of particles increases. In cases of double-diffusive sedimentation, our simulation results show little variation in the temperature-to-particle flux ratio among cases with various particle sizes and initial concentrations, which is consistent with previous theoretical derivations and experimental observations. The energy budget is analysed to show that the settling enhancement is a result of the thermal effect combined with shear dissipation and that the thermal contribution decreases as the size increases. Based on the balance of the energy budget, velocity scaling was derived for the quasi-steady state in the thermally controlled region, which can be used to characterize the plumes’ final velocity of double-diffusive sedimentation. Moreover, adopting some values from the simulation results yields a velocity criterion with which to distinguish different sedimentation patterns. Finally, we investigate changes in the particle-laden plumes below the region of the apparent temperature gradient at which secondary instabilities occur in the form of significant horizontal flow motion. We show that the resulting initial shift of the dominant modes can be approximated with the existing theoretical analysis of collective instabilities for salt fingers. A simple scaling argument for the change in the total cross-sectional area of particle-laden plumes is presented, which is then used to scale the resulting enhanced sedimentation.